Hans Walser, [20191119]
Mbiuskrper
Anregung: Ueli Wittorf, Zrich
1 Worum geht es?
Verallgemeinerung des Mbiusbandes auf Krper, deren Querschnitt ein regelm§iges Vieleck ist.
2 Erinnerung
Die Abbildung 1 zeigt ein gewhnliches geschlossenes Band. Seine zwei Seiten sind rot und blau gefrbt. Das Band ist in die Ebene abwickelbar.

Abb.1: Band
Wenn wir eine Torsion (Verdrehung) von 180¡ anbringen, erhalten wir ein Mbiusband (Abb.2). Es hat nur eine Seite und nur einen Rand. Wir knnen nicht mehr mit zwei verschiedenen Farben frben. Das Band hat eine negative Gau§sche Krmmung (Flchenkrmmung) und ist daher nicht in die Ebene abwickelbar.

Abb. 2a: Mbiusband

Abb. 2b: Sicht von oben
Allgemein erhalten wir bei einer Torsion von einem geraden Vielfachen von 180¡ (also einer Torsion von einem Vielfachen von 360¡) ein Band mit zwei Seiten und zwei Rndern. Wir knnen mit zwei Farben arbeiten. Die Abbildung 3 zeigt ein Beispiel mit einer Torsion von 6*180¡ = 1080¡. Es ist nicht in die Ebene abwickelbar.
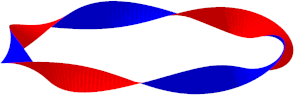
Abb. 3a: Torsion 6x180¡

Abb. 3b: Sicht von oben
Bei einem ungeraden Vielfachen von 180¡ als Torsion hat die Figur nur eine Seite und nur einen Rand. Die Abbildung 4 zeigt ein Beispiel mit einer Torsion von 5*180¡ = 900¡.

Abb. 4a: Torsion 5x180¡

Abb. 4b: Sicht von oben
3 Dreieckiger Querschnitt
Wir denken uns ein Dreikant-Prisma, welches wir zu einem Ring zusammenbiegen. Wenn wir das ãeinfach soÒ machen, knnen wir die drei Seiten des Prismas mit drei verschiedenen Farben versehen (Abb. 5). Die einzelnen Flchen sind Zylinderflchen (grn) oder Kegelflchen (rot und blau) und knnen in die Ebene abgewickelt werden.

Abb. 5: Zum Ring gebogenes Dreikant-Prisma
Wenn wir aber eine Torsion von 120¡ anbringen, sto§en falsche Farben aneinander (Abb. 6).
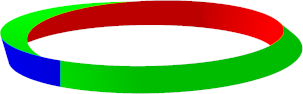
Abb. 6a: Torsion 120¡
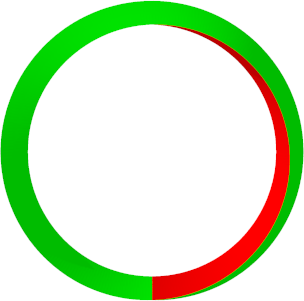
Abb. 6b: Sicht von oben
Wir mssen alle Flchen mit derselben Farbe einfrben (Abb. 7) und erhalten so eine einzige Flche. Sie ist nicht in die Ebene abwickelbar. Wir haben einen Mbiuskrper, der nur eine Kante hat.

Abb. 7a: Mbiuskrper

Abb. 7b: Sicht von oben
Die Abbildung 8 zeigt eine Spantenfigur zum Mbiuskrper. Die Spanten knnen mit elastischen Material, zum Beispiel nassem Papier, berzogen werden. So entsteht approximativ ein Mbiuskrper.
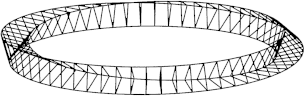
Abb. 8a: Spanten
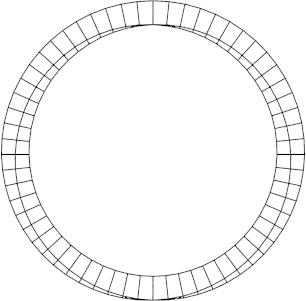
Abb. 8b: Sicht von oben
Bei einer Torsion von 240¡ ergeben sich dieselben Phnomene wie bei einer Torsion von 120¡.
Bei einer Torsion von 360¡ hingegen knnen wir wieder mit drei Farben arbeiten (Abb. 9). Die Flchen sind aber nicht in die Ebene abwickelbar.

Abb. 9a: Torsion 360¡
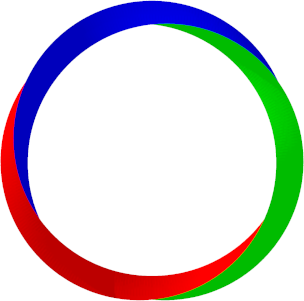
Abb. 9b: Sicht von oben
Allgemein gilt bei einem gleichseitigen Dreieck als Spant:
Torsion ![]() : Drei Farben mglich.
: Drei Farben mglich.
Torsion ![]() oder
oder ![]() : Nur eine Farbe mglich. Mbiuskrper.
: Nur eine Farbe mglich. Mbiuskrper.
Die
Abbildung 10 zeigt ein Beispiel fr ![]() . Wir knnen mit drei Farben arbeiten.
. Wir knnen mit drei Farben arbeiten.
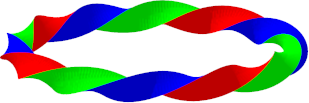
Abb. 10a: Torsion 1440¡
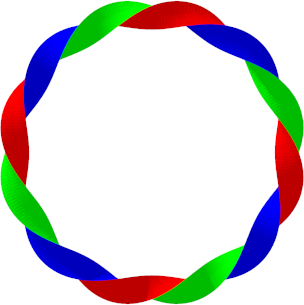
Abb. 10b: Torsion 1440¡
4 Allgemein
Wir nehmen ein regelm§iges n-Eck als Querschnitt, also als Spant.
Die
Torsion sei ![]() .
.
Dann
knnen wir mit ![]() Farben
arbeiten.
Farben
arbeiten.
Beispiel: Wir arbeiten mit einem regelm§igen Zwlfeck, also n = 12. Weiter sei m = 0. Die Abbildungen 11.0 bis 11.12 zeigen die Situation fr k von 0 bis 12, jeweils in der Sicht von oben. Die Anzahl der Kanten ist gleich der Anzahl der Farben.

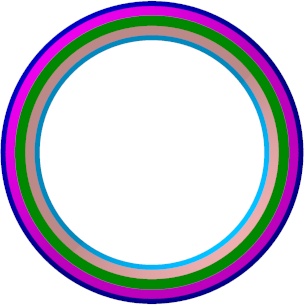
Abb. 11.0: Zwlf Farben


Abb. 11.1: Eine Farbe


Abb. 11.2: Zwei Farben


Abb. 11.3: Drei Farben


Abb. 11.4: Vier Farben


Abb. 11.5: Eine Farbe


Abb. 11.6: Sechs Farben


Abb. 11.7: Eine Farbe


Abb. 11.8: Vier Farben


Abb. 11.9: Drei Farben


Abb. 11.10: Zwei Farben


Abb. 11.11: Eine Farbe

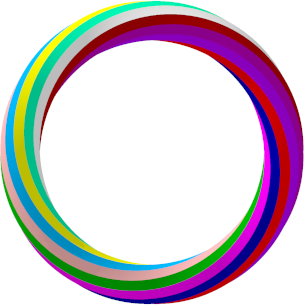
Abb. 11.12: Zwlf Farben
Die Abbildung 12 zeigt die Spanten fr die Abbildung 11.12 in einer Schrgansicht und von oben.
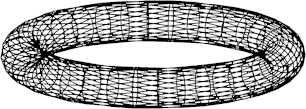
Abb. 12a: Spanten
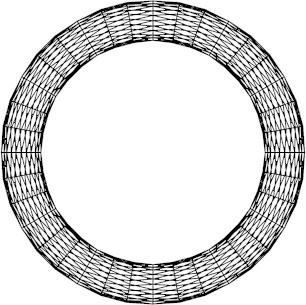
Abb. 12b: Sicht von oben
Weblinks
Hans Walser: Moebiusband breit
http://www.walser-h-m.ch/hans/Miniaturen/M/Moebiusband/Moebiusband.pdf
Hans Walser: Mbiusbnder
http://www.walser-h-m.ch/hans/Miniaturen/M/Moebius/Moebius.htm
Hans Walser: Mbiusband
http://www.walser-h-m.ch/hans/Miniaturen/M/Moebiusband2/Moebiusband2.htm
Hans Walser: Mbius-Band flechten
http://www.walser-h-m.ch/hans/Miniaturen/M/Moebius_Band_fl/Moebius_Band_fl.htm