Hans Walser, [20240703b]

Möndchen des Hippokrates

1 Worum es geht

Flächenverhältnis der beiden Möndchen des Hippokrates

2 Konstruktion

Zu einem rechtwinkligen Dreieck zeichnen wir die beiden Möndchen des Hippokrates. Wir verwenden zwei verschiedene Farben.

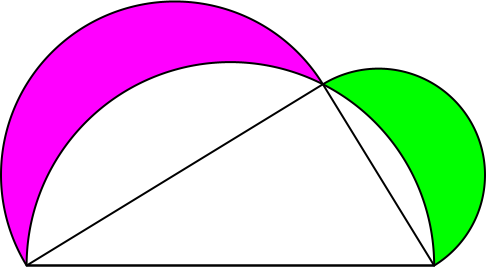
Abb. 1: Möndchen des Hippokrates

Nun versuchen wir, das rechtwinklige Dreieck mit einer vom rechten Winkel ausgehenden Geraden in zwei Teildreiecke im Flächenverhältnis der beiden Möndchenflächen zu teilen. Mit einiger Rechnung finden wir die Lösung (Abb. 2). Nach dem Satz des Hippokrates haben gleichfarbige Flächenteile denselben Flächeninhalt.

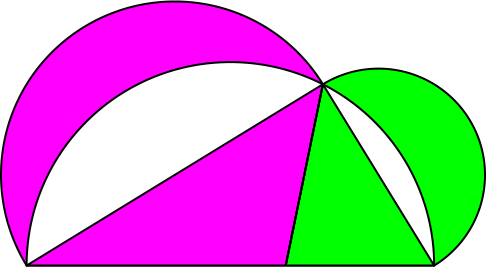
Abb. 2: Unterteilung im gleichen Flächenverhältnis

Die Abbildung 3 zeigt eine Animation dazu.

Abb. 3: Animation

3 Eine falsche Vermutung

Es sieht so aus, als ob die Trennlinie einen festen Drehpunkt habe. Diese Vermutung ist aber falsch (Abb. 4).

Abb. 4: Falsche Vermutung