Hans Walser, [20200510]

Monotone Krümmung

1 Worum geht es?

Kurven mit monoton wachsender Krümmung.

Insbesondere Klothoide.

2 Zollstock

Abb. 1: Zunehmende Richtungsänderung

Beim Gliedermaßstab (Zollstock, Doppelmeter) der Abbildung 1 wurde beim ersten Gelenk, also bei 20 cm, eine Richtungsänderung (also ein Außenwinkel) von 10° eingestellt, beim zweiten Gelenk eine Richtungsänderung von 20°, und so weiter. Beim letzten Gelenk, also bei 180 cm, haben wir eine Richtungsänderung von 90°. Wir erhalten eine einwärtslaufende eckige Spirale.

Frage 1: Wie kann die schrittweise zunehmende Richtungsänderung summarisch überprüft werden?

3 Krümmung

Statt einer schrittweise wachsenden Richtungsänderung können wir mit einer kontinuierlich zunehmenden Richtungsänderung arbeiten. Damit kommen wir zum Konzept der Krümmung. Diese ist die momentane Richtungsänderung. Die Krümmung kann beide Vorzeichen haben. Linkskurven haben eine positive, Rechtskurven eine negative Krümmung.

Der Kreis, der sich in einem Kurvenpunkt am besten der Kurve anschmiegt, heißt Krümmungskreis. Sein Radius ist der Kehrwert des Betrages der Krümmung. Je größer die Krümmung, umso schärfer die Kurve und entsprechend kleiner der Krümmungskreis.

Die Abbildung 2a zeigt die Klothoide. Die Krümmung der Klothoide wächst proportional zu deren Länge. Im Wendepunkt ist sie null, im rechten Ast positiv, im linken Astnegativ.

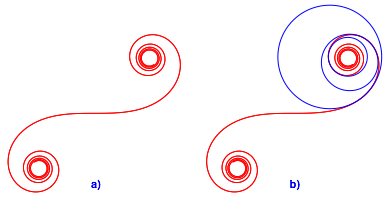
Abb. 2: Klothoide

In der Abbildung 2b sind exemplarisch drei Krümmungskreise eingezeichnet. Die Krümmungskreise haben keine Punkte gemeinsam.

4 Straßen- und Eisenbahnbau

Ein Kreis ist gleichmäßig gekrümmt. Beim Durchfahren eines Kreises haben wir daher eine konstante Radialbeschleunigung. Wenn wir jedoch von einem geraden Straßenstück abrupt in ein kreisförmiges Straßenstück einschwenken würden, ergäbe sich eine schlagartige Zunahme der Radialbeschleunigung. Um dies zu vermeiden, werden Straßen und Eisenbahntrassen so gebaut, dass die Krümmung und damit die Radialbeschleunigung allmählich zunehmen.

Frage 2: Welches war die kritische Stelle bei Großvaters Modelleisenbahn?

5 Eine optische Täuschung

Die Krümmungskreise schneiden sich nicht (Abb. 2b und 3a). Wenn wir diese aber dichter zeichnen, nehmen wir sie nicht mehr als Einzelkreise wahr. Hingegen glauben wir die nicht gezeichnete Klothoide zu sehen.

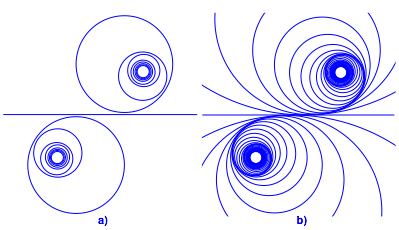
Abb. 3: Optische Täuschung

Frage 3: Warum erscheint in der Abbildung 3 eine Gerade als Krümmungs-„Kreis“?

6 Alle Klothoiden sind ähnlich

In allen drei Figuren der Abbildung 3 ist die Krümmung jeweils als lineare Funktion der Bogenlänge s mit dem Nullpunkt im Wendepunkt gewählt worden. Mit der Schreibweise

(1)

wurde in den Abbildungen 3a), 3b) und 3c) für a der Reihe nach 1, 2, und 3 gewählt. Man kann zeigen, dass alle Klothoiden ähnlich mit dem Skalierungsfaktor a sind.

Abb. 4: Die Klothoide

Die in der Abbildung 4 eingezeichneten so genannten Wickelpunkte sind durch gegeben.

Frage 4: Gibt es weitere geometrische Figuren, die jeweils zueinander ähnlich sind?

Die Abbildung 5 zeigt ein aus Klothoiden gebautes Kleeblatt.

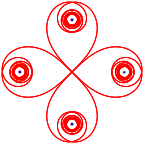
Abb. 5: Kleeblatt

7 Monoton wachsende Krümmung

Wir können (1) durch eine beliebige monotone Funktion ersetzen und erhalten dadurch jeweils eine Spirale.

In den Abbildungen 6a) und 6b) ist die Krümmungsfunktion eine Potenzfunktion in s vom zweiten beziehungsweise dritten Grad.

Abb.6: Krümmungsfunktionen zweiten und dritten Grades

In den Abbildungen 7a) und 7b) ist die Krümmungsfunktion exponentiell beziehungsweise logarithmisch. Der schwarze Punkt markiert den Nullpunkt der Streckenmessung.

Abb. 7: Krümmungsfunktion exponentiell und logarithmisch

Die Spirale der Abbildung 8b hat eine monoton wachsende Krümmung (Abb. 8a). Wir haben aber Stellen mit lokal konstanter Krümmung. Die Kurve „eiert“.

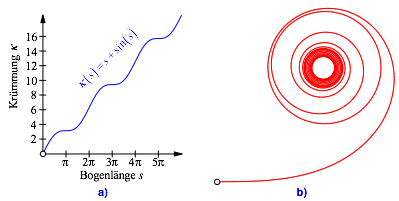
Abb. 8: Monoton wachsende Krümmung

Die Kurve der Abbildung 9b hat eine Krümmung (Abb. 9a).

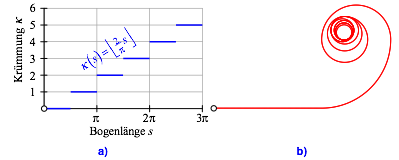
Abb. 9: Krümmungssprünge

Die Krümmung hat Sprünge. Sie ist zwar noch monoton wachsend, aber nicht mehr streng monoton wachsend. Die Kurve (Abb. 9b) besteht zunächst aus einem geraden Stück der Länge . Dann folgt mit einem Krümmungssprung ein Viertelkreis-Bogen mit dem Radius 1 und damit ebenfalls der Länge . Dann folgt ein Halbkreis-Bogen mit dem Radius und damit ebenfalls der Länge . Dann folgt ein Dreiviertelkreis-Bogen mit dem Radius , dann ein sich schließender voller Kreis mit dem Radius usw. Die Kurve ist keine Spirale mehr.

8 Bearbeitung der Fragen

Bearbeitung der Frage 1: Es ist 10° + 20° + … + 90° = 450°. Das letzte Gelenkglied muss also rechtwinklig zum ersten sein. Wir sehen, dass die Abbildung 1 nicht genau stimmt. Die Abbildung 10 zeigt die korrekte Situation. Zudem ist die Figur auch nach rückwärts gezeichnet. So ergibt sich eine Doppelspirale

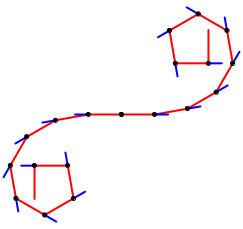
Abb. 10: Verlängerung nach rückwärts

Bearbeitung der Frage 2: Im Gleisoval pflegte die Lok beim Übergang vom geraden Gleisstück zum gebogenen Gleisstück (Abb. 11) aus den Schienen zu kippen.

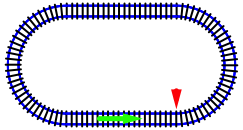
Abb. 11: Gleisoval und Gefahrenpunkt

Beim Übergang vom geraden Gleisstück zum gebogenen Gleisstück haben wir einen Krümmungssprung.

Bei Verwendung von Klothoidenbögen ändert die Krümmung stetig (Abb. 12).

Abb. 12: Kontinuierliche Krümmung

Bearbeitung der Frage 3: Im Wendepunkt haben wir die Krümmung null. Der zugehörige Krümmungskreis hat den Radius unendlich, ist also eine Gerade (nämlich die Wendetangente).

Bearbeitung der Frage 4: In der Ebene sind jeweils folgende Figuren zueinander ähnlich: Geraden, Kreise, Quadrate, regelmäßige Vielecke gleicher Eckenzahl, quadratische Parabeln, gleichseitige Hyperbeln.

Websites

Hans Walser: Klothoide

http://www.walser-h-m.ch/hans/Miniaturen/K/Klothoide/Klothoide.htm

Hans Walser: Krümmung

http://www.walser-h-m.ch/hans/Miniaturen/K/Kruemmung/Kruemmung.htm

Hans Walser: Krümmungen

http://www.walser-h-m.ch/hans/Miniaturen/K/Kruemmungen/Kruemmungen.htm

Hans Walser: Krümmung am Beispiel

www.walser-h-m.ch/hans/Miniaturen/B/Beispiel_zur_Kruemmung/Beispiel_zur_Kruemmung.htm

Hans Walser: Krümmung der Krümmung

www.walser-h-m.ch/hans/Miniaturen/K/Kruemmung_der_Kruemmung/Kruemmung_der_Kruemmung.htm