1 Das Problem

24 ganze Zahlen, welche eine arithmetische Folge bilden, sollen so in die Felder eines Mühlespiels (Abb. 1) gesetzt werden, dass sich bei jeder Mühle (drei durch eine gerade Linie verbundene Felder) dieselbe Summe s ergibt.

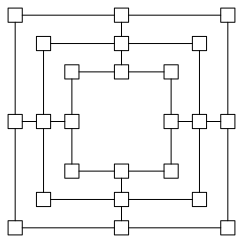
Abb. 1: Mühlespiel

2 Die Unlösung

Das Problem ist unlösbar.

3 Bearbeitung

Die 24 Zahlen sind von der Form

(1)

Zunächst kann die additive Konstante a weggelassen werden, da sie keinen Einfluss auf die Lösbarkeit des Problems hat.

Wenn es nun eine Lösung gibt, sind alle Zahlen Vielfache von b. Wir können also die Zahlen durch b dividieren. Daraus folgt: Wenn es eine Lösung gibt, gibt es auch eine Lösung mit

(2)

Nun ist (man beachte den Unterschied zwischen s und S):

(3)

Wir haben insgesamt 16 Mühlen. Jede Zahl kommt in genau zwei Mühlen vor. Somit ist:

(4)

Andrerseits muss s eine ganze Zahl sein. Widerspruch zu (4). Es gibt keine Lösung.

4 Variationen

Wir diskutieren einige Varianten zum Spielfeld der Abbildung 1. Wir werden sehen, dass sich für keine dieser Varianten das Zahlenproblem lösen lässt.

4.1 Beispiele

Die Abbildung 2 zeigt ein Beispiel mit „einteiliger“ Drehsymmetrie (also ohne Drehsymmetrie).

Abb. 2: Einteilige Drehsymmetrie

Im Beispiel der Abbildung 3 haben wir eine Punktsymmetrie.

Abb. 3: Punktsymmetrie

Im Beispiel der Abbildung 4 haben wir eine dreiteilige Drehsymmetrie und im Beispiel der Abbildung 5 eine fünfteilige Drehsymmetrie.

Abb. 4: Dreiteilige Drehsymmetrie

Abb. 5: Fünfteilige Drehsymmetrie

4.2 Unlösbarkeit

Für den Fall einer k-teiligen Drehsymmetrie haben wir:

(5)

Wir haben 4k Mühlen. Somit ist:

(6)

Die Mühlensumme s ist also immer echt halbzahlig. Widerspruch.