Hans Walser, [20110417a]
NatŸrliche Gleichung einer Kurve
1
Worum geht es?
Eine Kurve ist durch
Startpunkt, Startrichtung und die KrŸmmungsfunktion 
eindeutig
festgelegt. Dabei ist s die BogenlŠnge
der Kurve.
In der Praxis kann die
Kurve approximativ mit Turtle-Graphic gezeichnet werden.
Die expliziten
Beispiele bezeihen sich auf das CAS MuPAD.
2
Turtle-Graphic
Es wird eine
Strichzeichnung durch eine Folge von Bewegungskommandos an einen zeichnenden
Roboter (ãSchildkršteÒ) definiert.
Die beiden wichtigsten
Kommandos sind:
: Drehung
um den Winkel 
(Bogenma§,
positiver Drehsinn)
: VorwŠrtsbewegung
um d.
Die Startposition ist
standardmŠ§ig der Ursprung, die Startrichtung nach oben, also in Richtung der y-Achse. Wenn man lieber in Richtung der x-Achse startet, gibt man als erstes Bewegungskommando
ein.
Beispiel: Die
Befehlsfolge
Left(-PI/2),
Forward(1), Left(2*PI/5),
Forward(1), Left(2*PI/5),
Forward(1), Left(2*PI/5),
Forward(1), Left(2*PI/5),
Forward(1), Left(2*PI/5)
ergibt ein regelmŠ§iges
FŸnfeck der SeitenlŠnge 1. Das regelmŠ§ige FŸnfeck hat den Au§enwinkel 
, der hier als RichtungsŠnderung genommen werden muss.
NatŸrlich kann man die
fŸnf gleichen Befehlsfolgen zusammenfassen. Im folgenden das gesamte Programm
und das Ergebnis.
Fuenfeck:=plot::Turtle([Left(-PI/2),(Forward(1),
Left(2*PI/5))$5], LineWidth=1, LineColor=[1,0,0]):
plot(Fuenfeck, Scaling=Constrained,
Width=100, Height=100, Axes=Origin)
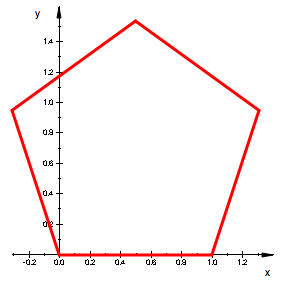
FŸnfeck
3
Die natŸrliche Gleichung
Wir definieren eine
RichtungsŠnderungsfunktion (KrŸmmungsfunktion) 
, welche von der BodenlŠnge s abhŠngt. Ferner legen wir eine SchrittlŠnge 
fest. Die Befehlsfolge
Left(-PI/2),(Forward(ds),
Left(kappa(n*ds)*ds))$n=0..N
ergibt die Kurve mit
dem Startpunkt im Ursprung, der Startrichtung in Richtung der x-Achse und der KrŸmmungsfunktion 
.
4
Beispiele
FŸr 
ergibt sich eine
Gerade.
FŸr 
ergibt sich ein
Kreisbogen mit dem Radius 
.
kappa:=s->2:
Laenge:=2:
ds:=0.001:
N:=round(Laenge/ds):
Kurve:=plot::Turtle([Left(-PI/2),(Forward(ds),
Left(kappa(n*ds)*ds))$n=0..N],
LineWidth=1, LineColor=[1,0,0]):
plot(Kurve, Scaling=Constrained,
Width=100, Height=100, Axes=Origin)
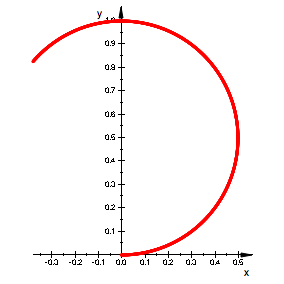
Kreisbogen
FŸr 
erhalten wir die
Standard-Klothoide.
kappa:=s->s:
Laenge:=6:
ds:=0.001:
N:=round(Laenge/ds):
Kurve:=plot::Turtle([Left(-PI/2),(Forward(ds),
Left(kappa(n*ds)*ds))$n=0..N],
LineWidth=1, LineColor=[1,0,0]):
plot(Kurve, Scaling=Constrained,
Width=100, Height=100, Axes=Origin)
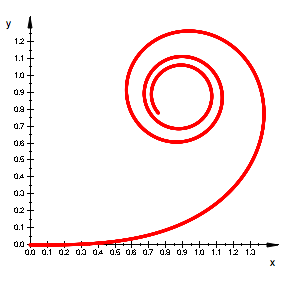
Klothoide
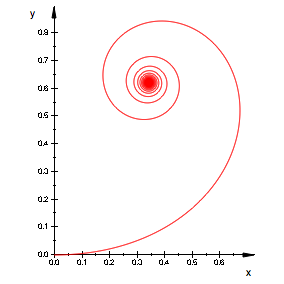
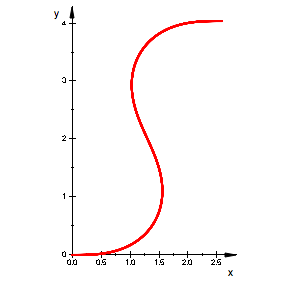
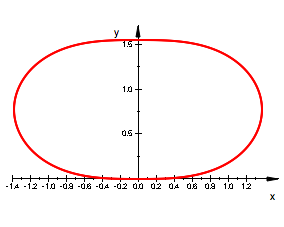
Weitere Beispiele ohne
Kommentar.
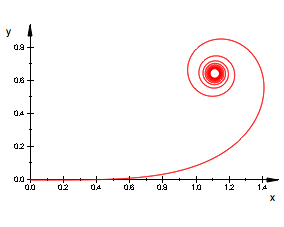
