Hans Walser, [20150608]

Negative Dimensionen

1 Die Frage

Anlässlich eines Workshops über höherdimensionale Hyperwürfel stellte ein Schüler die Frage, ob es auch Würfel der Dimension –1 gebe.

Wir denken zunächst über Hyperwürfel mit positiven ganzzahligen Dimensionen nach und versuchen dann Verallgemeinerungen.

2 Hyperwürfel mit positiven Dimensionen

2.1 Anzahl der Bauteile

Die Tabelle 1 ist die Bauteiltabelle für Hyperwürfel.

Die Dimension des Hyperwürfels wird mit n bezeichnet. Für n = 0, n = 1 und n = 2 sind die Sonderbezeichnungen Punkt, Strecke und Quadrat geläufig.

Mit k bezeichnen wir die Bauteildimension.

n\k	0	1	2	3	4	5
0	1
1	2	1
2	4	4	1
3	8	12	6	1
4	16	32	24	8	1
5	32	80	80	40	10	1

Tab. 1: Bauteile

Lesebeispiel: Der gewöhnliche Würfel ist dreidimensional, also ist n = 3. Er hat 8 Ecken (Dimension k = 0), 12 Kanten (Dimension k = 1), 6 Seitenquadrate (Dimension k = 2) und schließlich einmal sich selber (Dimension k = 3).

2.2 Bezeichnungen

Mit bezeichnen wir im n-dimensionalen Hyperwürfel die Anzahl der Bauteile der Dimension k. Die sind also die Einträge der Tabelle 1.

Die nach unten offene Dreiecksmatrix der bezeichnen wir mit B.

2.3 Rekursion

Es gilt die Rekursion:

Herleitung durch eine geometrische Überlegung: Kopieren und Verschieben in eine weitere freie Richtung, die zu den bisherigen Richtungen orthogonal ist.

2.4 Link zu den Binomialkoeffizienten

Weglassen des Faktors 2 in der Rekursion gibt die Rekursion der Binomialkoeffizienten.

Wenn wir mit P die nach unten offene Dreiecksmatrix der Binomialkoeffizienten verstehen (Pascal-Dreieck), gilt:

2.5 Explizite Formel

Es gilt:

Hier zeigt sich erneut ein Link zu den Binomialkoeffizienten.

2.6 Zeilensummen

Es ist:

Vergleiche dazu:

2.7 Alternierende Zeilensummen

Es ist:

Wir haben eine Invariante. Im Prinzip ist das die Euler-Charakteristik.

2.8 Link zur binomischen Formel

Es ist:

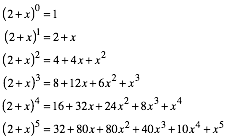
Wir sehen, wie der Hase läuft. Die Koeffizienten sind die Einträge aus unserer Bauteiltabelle. Die Potenzen der x entsprechen den Dimensionen der Bauteile.

Allgemein ist:

Die Abbildung 1 zeigt die Grafen für .

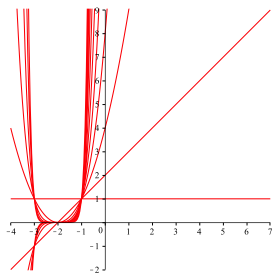
Abb. 1: Grafen

3 Ganze Dimension

Nun sei n eine ganze Zahl. Sie kann also auch negativ sein.

3.1 Bauteiltabelle

Die explizite Formel funktioniert auch in diesem Fall.

Wir erhalten damit:

n\k	0	1	2	3	4	5
0	1
1	2	1
2	4	4	1
3	8	12	6	1
4	16	32	24	8	1
5	32	80	80	40	10	1

Tab. 2: Bauteile

3.2 Warum funktioniert das?

Der kritische Punkt sind die Binomialkoeffizienten. Wir können diese wie folgt definieren und berechnen:

Diese Formel funktioniert für beliebiges , insbesondere also auch für negative ganze Zahlen n. Allerdings haben wir in diesem Fall keinen Faktor null im Zähler, die Formel funktioniert daher für beliebig große k. Daher ergibt sich im oberen Teil der Tabelle 2 keine Dreiecksmatrix. Es wird der ganze Quadrant ausgefüllt.

3.3 Rekursion

In der Tabelle 2 der Bauteile gilt die Rekursion auch im oberen Teil und insbesondere beim Übergang vom oberen Teil zum unteren Teil. Der Autor gesteht, dass er zunächst mit dieser Rekursion und Rückwärtsrechnen den oberen Teil der Tabelle 2 bestimmt hat.

3.4 Zeilensummen

Aus der Tabelle 2 erhalten wir für die Zeilensumme (nun eine Reihe):

Das passt zur Zeilensumme .

Für wird die Zeilensumme spannend:

CAS gibt den Wert , aber das wollen wir nun selber berechnen. Dazu arbeiten wir mit der formalen Potenzreihe:

Wir leiten links und rechts ab:

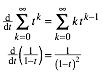
Vergleich ergibt:

Einsetzen von liefert:

Die Rechnerei hätten wir uns allerdibgs sparen können: Wegen der Rekursionsformel ist eine Zeilensumme jeweils das Dreifache der Zeilensumme der darüber liegenden Zeile.

3.5 Alternierende Zeilensumme

Aus der Tabelle 2 ergibt sich für die alternierende Zeilensumme:

Die Euler-Charakteristik stimmt also auch hier.

Für wird die Sache trickier. Wir verwenden wieder die Formel:

und erhalten für :

Wer Lust hat, kann die Euler-Charakteristik für oder gar allgemein nachrechnen.

3.6 Schrägzeilensummen

Wir rechnen im oberen Teil der Tabelle 2 von links oben nach rechts unten mit der Steigung –1. Da haben wir ja schon längst die Binomialkoeffizienten entdeckt.

Für die Schrägzeilensumme erhalten wir (mit der Ausnahme der untersten Schrägzeile) den Wert null.

Für die alternierende Schrägzeilensumme erhalten wir durchgehend den Wert .

3.7 Taylor

Die Einträge in der Bauteiltabelle treten auch als Koeffizienten in Taylor-Entwicklungen auf. Die Beziehung

kann auf negative n übertragen werden. Es gilt für negative ganze Zahlen n:

Wir müssen mit Taylor-Entwicklungen arbeiten.

Beispiele:

Für n = –1 erhalten wir:

Für n = –2 erhalten wir:

Die Abbildung 2 zeigt die Grafen für .

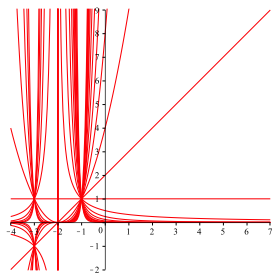
Abb. 2: Grafen auch für negative Exponenten

4 Link mit den Binomialkoeffizienten

Die Tabelle 3 zeigt die Binomialkoeffizienten auch für negative Werte von n.

n\k	0	1	2	3	4	5
	1		21		126
	1		15		70
	1		10		35
	1		6		15
	1		3		5
	1		1		1
0	1
1	1	1
2	1	2	1
3	1	3	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1

Tab. 3: Binomialkoeffizienten

Die übliche Rekursion der Binomialkoeffizienten gilt auch im oberen Teil und insbesondere beim Übergang vom oberen Teil zum unteren Teil.

Wir erkennen im oberen Teil ein „schräges“ und alternierend mit Minuszeichen versehenes Pascaldreieck.

Für die Zeilensumme gilt ja im Pascaldreieck die Formel . Da haben wir im negativen Teil etwas Mühe. Für ergibt sich die Zeilensumme:

Das führt zum berühmten Dialog zwischen Silvia und Silvio:

Silvia fasst in Zweiergruppen zusammen und erhält null:

Silvio macht dasselbe, lässt aber die vorderste 1 stehen:

Wer hat Recht? In einer Konkordanzdemokratie würde man den salomonischen Mittelwert aushandeln. Das ist erst noch der erwartete Wert .

Wir können auch die Formel für geometrische Reihen anwenden:

Das gibt zwar auch den erwarteten Wert , ist aber etwas abenteuerlich. Wir reiten auf dem Konvergenzradius.

Interessant ist, dass wir bei der Bauteiltabelle (Tabelle 2) keine derartigen Probleme mit der Konvergenz haben.

5 Hyperwürfel mit Dimension –1

Gemäß der Tabelle 2 besteht der Hyperwürfel der Dimension –1 aus folgenden Bauteilen:

Also:

Voilà.

Der Autor gesteht, dass er sich das auch nicht vorstellen kann.

6 Ausblick: Gebrochene Dimensionen

Die Taylor-Entwicklung können wir natürlich auch für gebrochene Exponenten vornehmen. Im Folgenden zwei Beispiele.

6.1 Dimension ½

Für ergibt sich:

Dabei definieren wir:

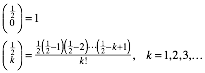
In Zahlen:

Am Anfang ist das alternierende Vorzeichen gestört. Das ist aber korrekt so.

6.2 Dimension –1/2

Für ergibt sich:

In Zahlen:

Der Vergleich mit der Dimension ½ ist interessant.