Hans Walser, [20191210]
Negative Dimensionen
Anregung: Z. D., W.
1 Worum geht es?
AnlŠsslich eine Workshops mit SchŸlerinnen und SchŸlern Ÿber hyperdimensionale WŸrfel wurde die Frage gestellt, ob es auch einen HyperwŸrfel der Dimension –1 gebe.
2 €hnlichkeits-Dimension
2.1 Definition
Wir verwenden folgenden Dimensions-Begriff:
Fguren, die aus N mit dem €hnlichkeitsfaktor r vergrš§erten oder verkleinerten Kopien ihrer selbst bestehen, hei§en selbstŠhnlich.
FŸr diese Figuren gilt die €hnlichkeitsdimension D:
(1)
2.2 Beispiel
Bei einem
Quadrat erhalten wir fŸr 
insgesamt N = 4 Kopien (Abb. 1).
Abb. 1: Quadrat und vier Kopien
Nach (1) ergibt sich die Dimension D:
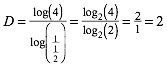(2)
Das Quadrat ist zweidimensional.
3 Punktfolge
3.1 Zwei Farben
Wir gehen aus von der unendlich langen Punktfolge der Abbildung 2a. Man kann sich darunter zum Beispiel die Menge der ganzen Zahlen auf dem Zahlenstrahl vorstellen.
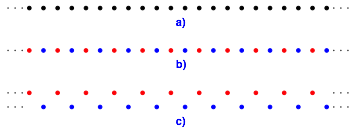
Abb. 2: Punktfolge
Nun fŠrben wir die Punkte im Wechsel rot und blau (Abb. 2b). Man kann sich darunter die geraden beziehungsweise die ungeraden ganzen Zahlen vorstellen.
Wir erhalten so zwei Punktfolgen (Abb. 2c), welche aus der ursprŸnglichen Punktfolge durch eine Streckung mit dem Faktor 2 hervorgehen. FŸr die Berechnung der €hnlichkeitsdimension D nach (1) ist also N = 2 und r = 2, und daher:
(3)
Die Punktfolge hat die negative Dimension –1.
3.2 Drei Farben
Wir kšnnen auch mit drei Farben arbeiten (Abb. 3).
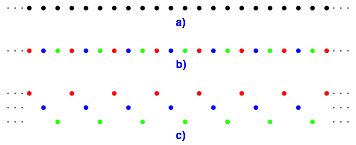
Abb. 3: Drei Farben
Zahlentheoretisch sind das die Restklassen modulo 3.
FŸr die Dimensionsberechnung nach (1) ist N = 3 und r = 3 und daher:
(4)
Wir erhalten wiederum die Dimension –1.
4 Gitterpunkte in der Ebene
4.1 Vier Farben
Wir beginnen mit den Gitterpunkten eines unendlich gro§ gedachten Quadratgitters (Abb. 4a).
Abb. 4: Gitterpunkte
Wir kšnnen mit vier Farben so fŠrben, dass wir vier Punktgitter erhalten, die zum Ausgangspunktgitter Šhnlich sind mit dem Streckfaktor 2. Es ist also N = 4 und r = 2 und daher:
(5)
Wir erhalten die €hnlichkeitsdimension –2.
4.2 Zwei Farben
Die Abbildung 5b zeigt eine FŠrbung mit nur zwei Farben, im Wechsel rot und blau.
Abb. 5: Zwei Farben
Wir erkennen zwei diagonale Punktgitter (Abb. 6).
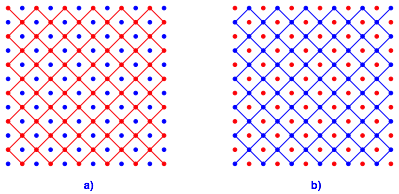
Abb. 6: Diagonale Punktgitter
Die
beiden Punktgitter sind gegenŸber dem Original (Abb. 5a) um 
gedreht
und mit dem Faktor 
gestreckt
und damit zu diesem Šhnlich.
FŸr die €hnlichkeitsdimension erhalten wir:
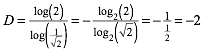(6)
Wir haben nach wie vor die €hnlichkeitsdimension –2.
4.3 FŸnf Farben
In der Abbildung 7b wurden fŸnf Farben verwendet.
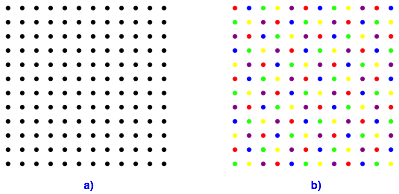
Abb. 7: FŸnf Farben
Wir erkennen fŸnf schrŠge Quadratraster. In der Abbildung 8 sind zwei der fŸnf schrŠgen Quadratraster eingezeichnet.
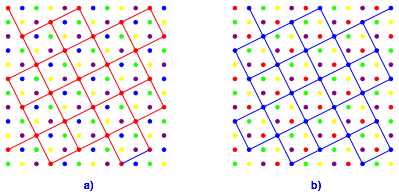
Abb. 8: SchrŠge Quadratraster
Die
schrŠgen Raster sind zueinander parallel und haben die Maschenweite 
. Die zugehšrigen Gitter gehen daher aus dem
Originalgitter durch eine Drehstreckung mit dem Streckfaktor 
hervor.
Der Drehwinkel ist 
. FŸr die €hnlichkeitsdimension finden wir:
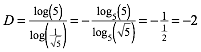(7)
Man sieht, wie der Hase lŠuft.
5 Allgemein
Die Menge der Gitterpunkte eines n-d-HyperwŸrfelgitters hat die €hnlichkeitsdimension D = –n.
6 Ausblick und Frage
Die Fraktale haben positive, aber in der Regel nicht ganzzahlige (meist sogar irrationale) €hnlichkeitsdimensionen. Gibt es Entsprechendes im negativen Bereich?
Websites
Wikipedia: Fraktale Dimension (10.12.2019)