Hans Walser, [20110705a]
Neunecksapproximation
Anregung: T. W., L.
1 Worum geht es?
Es wird ein Verfahren gezeigt, wie in einem regulŠren 48-Eck mit Hilfe von Diagonalen eine Approximation des regulŠren Neunecks gezeichnet werden kann.
2 Das regulŠre 48-Eck
Die Abbildung 1 zeigt die Eckpunkte des regulŠren 48-Ecks.

Abb. 1: Das regulŠre 48-Eck
3 Erster Konstruktionsschritt
Als Schnittpunkte von geeigneten Diagonalen erhalten gemŠ§ Abbildung 2 wir sechs der neun Eckpunkte der gesuchten Figur.
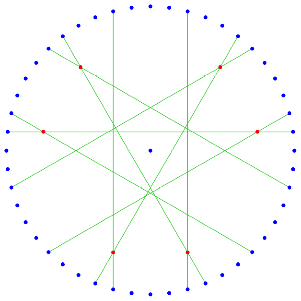
Abb. 2: Erster Schritt: 6 von 9 Punkten
4 Zweiter Konstruktionsschritt
Die restlichen drei Eckpunkte erhalten wir als Schnittpunkte weiterer Diagonalen gemŠ§ Abbildung 3.
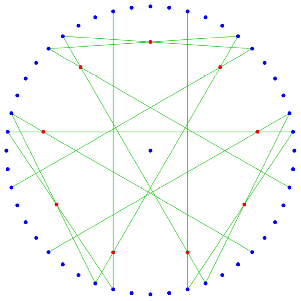
Abb. 3: Zweiter Schritt: Restliche Punkte
5 Neuneck
In der Abbildung 4 ist das Neuneck eingezeichnet.
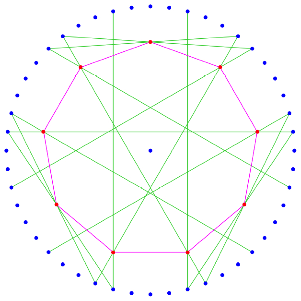
Abb. 4: Neuneck
6 Genauigkeit
Nach einem Satz von Gau§ gibt es keine exakte Konstruktion des regelmŠ§igen Neunecks mit Zirkel und Lineal. Unsere Konstruktion ist also fehlerhaft.
Bei einem exakten Neuneck messen die Zentriwinkel je 40ˇ, die neun Eckpunkte liegen auf einem Kreis.
Bei unserer NŠherungskonstruktion messen die Zentriwinkel zwischen zwei benachbarten Punkten des ersten Konstruktionsschrittes 40.091319734392ˇ. Diese Winkel sind also etwas zu gro§.
Die restlichen Zentriwinkel messen je 39.954340132804ˇ.
Die neun Punkte liegen nicht auf einem Kreis. Die drei Punkte des zweiten Konstruktionsschrittes haben vom Mittelpunkt einen Abstand, der nur 99.7840985930699% des Abstandes der sechs Punkte des ersten Konstruktionsschrittes betrŠgt.