Hans Walser, [20181001]

Neunen

1 Worum geht es?

Teilbarkeit von Dezimalzahlen durch 9, 99, 999, ... .

2 Teilbarkeit durch 9

In der Schule lernt man, dass eine Dezimalzahl genau dann durch 9 teilbar ist, wenn ihre Ziffernsumme durch 9 teilbar ist.

2.1 Beweis

Die Zahl z bestehe im Dezimalsystem aus den l Ziffern z_l–1, z_l–2, ... , z₀. Dabei ist z₀ die Anzahl der Einer, z₁ die Anzahl der Zehner und allgemein z_j die Anzahl der Summanden . Somit ist:

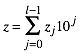(1)

Wir formen die Summanden in (1) um. Zunächst ist:

(2)

Weiter ist nach der verallgemeinerten dritten binomischen Formel:

(3)

Der Ausdruck ist also durch 9 teilbar. Damit wird:

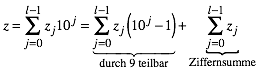(4)

Die Zahl z ist also genau dann durch 9 teilbar ist, wenn die Ziffernsumme durch 9 teilbar ist. Allenfalls kann das Kriterium iteriert werden, bis schließlich die Ziffernsumme 9 entsteht.

In einem beliebigen Positionssystem mit der Basis b übernimmt die Ziffer für b – 1 die Rolle der Neun. Es gelten dann entsprechende Teilbarkeitsregeln. Der Beweis geht analog, die Zahl 10 muss durch b ersetzt werden.

2.2 Beispiele

a) Ist 16180339887499 durch 9 teilbar?

Wir erhalten die Ziffernsumme:

1 + 6 + 1 + 8 + 0 + 3 + 3 + 9 + 8 + 8 + 7 + 4 + 9 + 9 = 76

Wir müssen nun prüfen, ob die Ziffernsumme 76 durch 9 teilbar ist. Wer wie ich eine Zahlenphobie hat, bildet erneut die Ziffernsumme:

7 + 6 = 13

Und nochmals:

1 + 3 = 4

Da 4 von 9 verschieden ist, ist die Zahl 16180339887499 nicht durch 9 teilbar.

b) Ist 16185339887499 durch 9 teilbar?

Wir erhalten die Ziffernsumme:

1 + 6 + 1 + 8 + 5 + 3 + 3 + 9 + 8 + 8 + 7 + 4 + 9 + 9 = 81

Wir müssen nun prüfen, ob die Ziffernsumme 81 durch 9 teilbar ist. Wer wie ich eine Zahlenphobie hat, bildet erneut die Ziffernsumme:

8 + 1 = 9

Nun haben wir die Neun. Die Zahl 16185339887499 ist durch 9 teilbar.

Dieses Verfahren kann verallgemeinert werden.

3 Verallgemeinerung

Zunächst Beispiele

3.1 Teilbarkeit durch 99

a) Ist 716180339887499 durch 99 teilbar?

Wir unterteilen die Zahl von rechts her in zweistellige Summanden:

7 + 16 + 18 + 03 + 39 + 88 + 74 + 99 = 344

Nun müssen wir prüfen, ob 344 durch 99 teilbar ist. Wer wie ich eine Zahlenphobie hat, wiederholt das Verfahren:

3 + 44 = 47

Da 47 von 99 verschieden ist, ist die Zahl 716180339887499 nicht durch 99 teilbar.

b) Ist 716185539887499 durch 99 teilbar?

Wir unterteilen die Zahl von rechts her in zweistellige Summanden:

7 + 16 + 18 + 55 + 39 + 88 + 74 + 99 = 396

Nun müssen wir prüfen, ob 396 durch 99 teilbar ist. Wer wie ich eine Zahlenphobie hat, wiederholt das Verfahren:

3 + 96 = 99

Nun haben wir die 99. Die Zahl 716185539887499 ist durch 99 teilbar.

3.2 Teilbarkeit durch 999

a) Ist 3716180339887499 durch 999 teilbar?

Wir unterteilen die Zahl von rechts her in dreistellige Summanden:

3 + 716 + 180 + 339 + 887 + 499 = 2624

Nun müssen wir prüfen, ob 2624 durch 999 teilbar ist. Wer wie ich eine Zahlenphobie hat, wiederholt das Verfahren:

2 + 624 = 626

Da 626 von 999 verschieden ist, ist 3716180339887499 nicht durch 999 teilbar.

b) Ist 3716553339887499 durch 999 teilbar?

Wir unterteilen die Zahl von rechts her in dreistellige Summanden:

3 + 716 + 553 + 339 + 887 + 499 = 2997

Nun müssen wir prüfen, ob 2997 durch 999 teilbar ist. Wer wie ich eine Zahlenphobie hat, wiederholt das Verfahren:

2 + 997 = 999

Nun haben wir die 999. Die Zahl 3716553339887499 ist durch 999 teilbar.

Wir sehen, wie der Hase läuft.

3.3 Einfacher Beweis

Wir denken uns die Schreibweisen 00, 01, ... , 99 als Ziffernsymbole in einem Positionssystem mit der Basis 100. Die psychologische Schwierigkeit dieser Überlegung besteht darin, Symbole aus zwei grafisch getrennten Zeichen als ein einziges Ziffernsymbol zu sehen. Bei Buchstaben haben wir uns zwar daran gewöhnt. Das Pünktchen auf dem i ist mit dem Rest des Zeichens grafisch nicht verbunden.

Die Zahl

7 16 18 55 39 88 74 99

besteht also auch 99 Einern, 74 Hundertern, 88 Zehntausendern, 39 Millionen etc. Zehner gibt es nicht.

Die Ziffernsumme ist dann:

7 + 16 + 18 + 55 + 39 + 88 + 74 + 99 = 3 96

In diesem Zahlensystem mit der Basis 100 spielt die 99 die Rolle der 9 im Dezimalsystem.

Analog in einem Zahlensystem mit der Basis 100 und den Ziffern 000, 001, ... , 999. Etc.

3.4 Formaler Beweis

Nun wieder zurück ins Dezimalsystem. Wir prüfen die Teilbarkeit einer gegebenen Zahl z durch eine Zahl, die aus s Neunen besteht.

Wir unterteilen die Zahl von rechts her in s-stellige Summanden. Allenfalls werden ganz links Nullen vorgehängt.

Dazu schreiben wir die Zahl z in der Form:

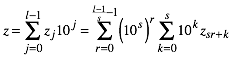(5)

Die Abbildung 1 versucht, die Situation mit den Zehnerpotenzen für s = 3 zu illustrieren.

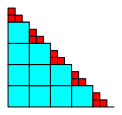
Abb. 1: Zehnerpotenzen

Weiter ist nach der verallgemeinerten dritten binomischen Formel:

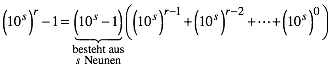(6)

Damit erhalten wir aus (5):

(7)

Somit ist die Zahl z genau dann durch die aus s Neunen bestehende Zahl teilbar, wenn dies für die Summe der s-stelligen Zahlen der Fall ist.