Hans Walser, [20190729]

Nullstellen

1 Worum geht es?

Wir beschreiben eine Funktion mit einer merkwürdigen Nullstellenverteilung.

Die Funktion erscheint in [1].

2 Einstiegsbeispiel

Die Abbildung 1 gibt den Grafen der Funktion:

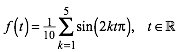(1)

Da die Funktion periodisch mit der Periodenlänge 1 ist, genügt ein entsprechender Ausschnitt.

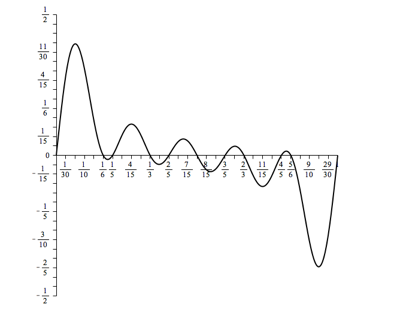
Abb. 1: Verteilung der Nullstellen?

Wir haben Nullstellen bei:

(1)

Wir können die Nullstellen aber in zwei Kategorien aufteilen:

und (2)

Damit haben wir eine Struktur gefunden. Die Nullstellen sind entweder Vielfache von oder Vielfache von . Die Abbildung 2 versucht, diesen Sachverhalt zu illustrieren.

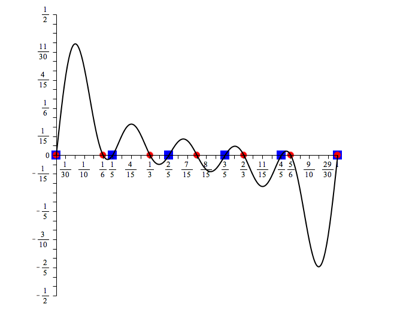
Abb. 2: Zwei Kategorien von Nullstellen

3 Beweisskizze

Wir wählen exemplarisch . In den Sinusfunktionen von (1) haben wir dann die Eingabewerte . Die Abbildung 3 zeigt die Situation auf dem Einheitskreis. Die zugehörigen Sinuswerte annullieren sich.

Abb. 3: t = 3/5

Für andere Vielfache von einem Fünftel geht die Überlegung analog.

Nun wählen wir . Die Abbildung 4 zeigt die Situation auf dem Einheitskreis.

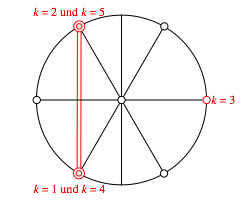
Abb. 4: t = 4/6

Die zugehörigen Sinuswerte annullieren sich. Das „Fehlen“ von k = 6 spielt keine Rolle.

Schließlich wählen wir . Die Abbildung 5 zeigt die Situation auf dem Einheitskreis.

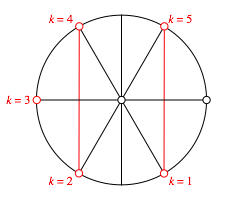
Abb. 5: t = 5/6

Wir haben wieder eine Annullierung der Sinuswerte. Das „Fehlen“ von k = 6 spielt keine Rolle.

Analog für die restlichen Vielfachen von einem Sechstel.

4 Allgemein

Zu gegebenem n hat die Funktion

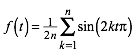(3)

Nullstellen bei Vielfachen von und bei Vielfachen von .

Der Koeffizient dient nur dazu, die Darstellung zu vereinfachen. Auf die Nullstellen hat er keinen Einfluss.

5 Beispiele

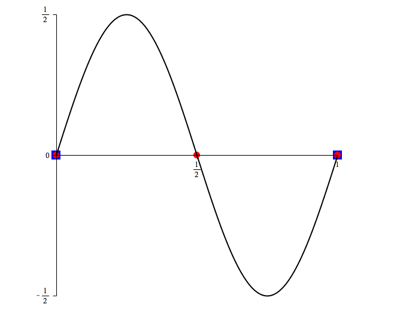
Abb. 6.1: n = 1

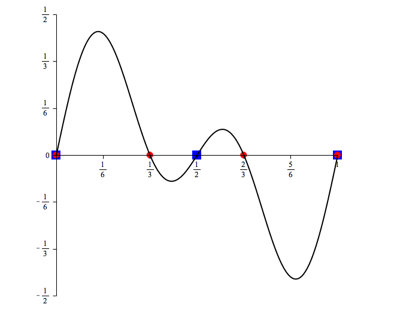
Abb. 6.2: n = 2

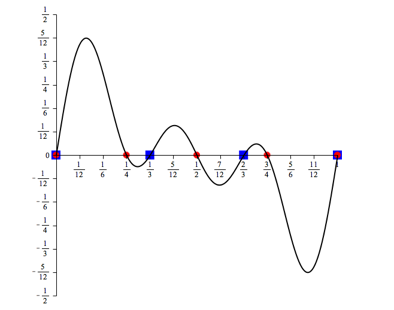
Abb. 6.3: n = 3

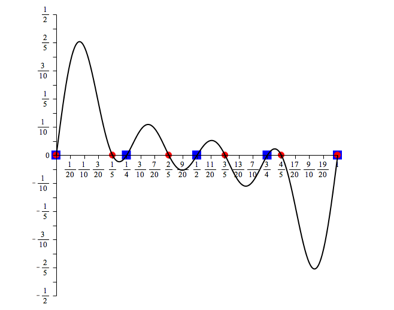
Abb. 6.4: n = 4

Website

[1] Hans Walser: Herzkurve

http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve5/Herzkurve5.htm