Hans Walser, [20130621]
n-Sektrix
Anregung: H. M.-S., V.
1 Worum es geht
Die Trisektrix wird verallgemeinert.
Es seien zwei Punkte A und B gegeben. Sie werden zum Dreieck ABC ergŠnzt, so dass:
Die n-Sektrix ist der geometrische Ort der Punkte C.
Es zeigen sich ZusammenhŠnge mit regelmŠ§igen Vielecken.
Es werden Fakten und PhŠnomene aufgelistet, ohne Beweis.
2 Beispiele
In den
folgenden Beispielen wird 
und 
gewŠhlt. Die
beiden Punkte sind die SchlŸsselpunkte und werden immer blau markiert.
2.1 Monosektrix
Der Pedanterie halber: FŸr n = 1 sind a und b parallel, der Punkt C ein uneigentlicher Punkt und die Monosektrix die uneigentliche Gerade.
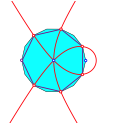
2.2 Bisektrix
FŸr n = 2 ergibt sich ein Kreis.
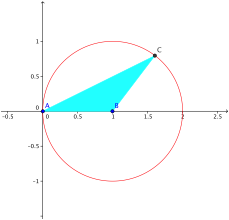
Bisektrix
Die Bisektrix-Dreiecke sind gleichschenklig mit Spitze in B.
Der
rechte Schnittpunkt mit der x-Achse
ist bei 
.
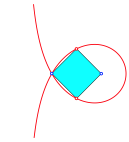
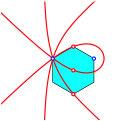
2.3 Trisektrix
FŸr n = 3 ergibt sich die Trisektrix.
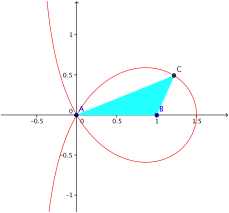
Trisektrix
Die Trisektrix hat folgende Eigenschaften:
Der
rechte Schnittpunkt mit der x-Achse
ist bei 
.
Es ist 
.
Koordinatengleichung:
|
|
|
|
|
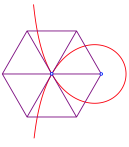
Quadrat |
Hexagon |
FŸnfeck und
Zehneck |
RegelmŠ§ige Vielecke
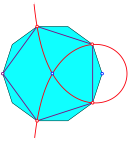
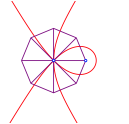
2.4 4-Sektrix
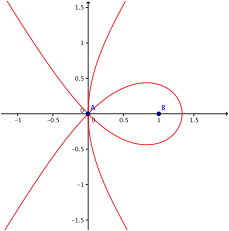
4-Sektrix
Der
rechte Schnittpunkt mit der x-Achse
ist bei 
.
|
|
|
|
|
FŸnfeck |
Achteck |
Siebeneck und
14-Eck |
RegelmŠ§ige Vielecke
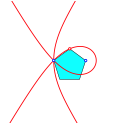
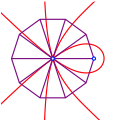
2.5 5-Sektrix
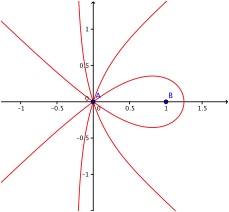
5-Sektrix
Der
rechte Schnittpunkt mit der x-Achse
ist bei 
.
|
|
|
|
|
Sechseck |
Zehneck |
Neuneck und 18-Eck |
RegelmŠ§ige Vielecke
Wir sehen, wie der Hase lŠuft.