Hans Walser, [20130116]
Null hoch null
Anregung: S.M.S., B.
Frage
Was ergibt 
? — Immerhin ergibt 
immer 1 und 
immer 0... .
Bearbeitung
1 Experimente mit Taschenrechnern
Sharp PC-1211 liefert: 
Texas Instruments TI-31 SOLAR liefert Error.
Der Rechner in meinem
Computer liefert: 
Der Google-Rechner
liefert: 
Wir haben eine ganze Palette von Ergebnissen.
2 Hoch null
Die Frage nach 
wird wie folgt
bearbeitet:
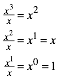
Wir kommen also zu 
durch Dividieren.
Es wird durch x dividiert. Nun ist
aber eine Division nur sinnvoll, wenn der Divisor nicht null ist. Man kann
nicht durch null dividieren. Das hei§t aber, 
gilt nur fźr 
.
Mit andern Worten: 
ist nicht
sinnvoll. Es ist ăverbotenŇ so wie auch die Division durch null ăverbotenŇ ist.
3 AnnŠherung an null
Wir berechnen 
fźr x-Werte, die gegen Null streben.
|
x |
x^x |
|
0.1 |
0.7943282347 |
|
0.01 |
0.9549925860 |
|
0.001 |
0.9931160484 |
|
0.0001 |
0.9990793900 |
|
0.00001 |
0.9998848774 |
|
0.000001 |
0.9999861846 |
|
0.0000001 |
0.9999983882 |
|
0.00000001 |
0.9999998158 |
Wir vermuten: 
Beweis: ZunŠchst ist:
Daraus ergib sich:
Wir bearbeiten den Exponenten. Mit der Regel von Bernoulli-de lŐH™pital erhalten wir:
Somit ist:
Die Funktion 
ist fźr 
nicht definiert,
es ist aber 
. Die Abbildung zeigt den Grafen der Funktion.
Funktionsgraf
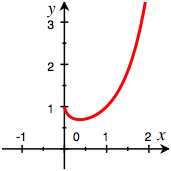
Die folgende Abbildung
zeigt den Funktionsgrafen von 
. Diese Funktion ist auf 
definiert.
Erweiterung der Funktion