Hans Walser, [20190419]
OberflŠchengleiche Tetraeder und Oktaeder
Anregung: Patrik G. K. Wiesner, BSc ETHZ, Davidgasse 42, A - 1100 Wien
1 Worum geht es?
Wir suchen eine gemeinsame Zerlegung der OberflŠchen eines Tetraeders und eines Oktaeders mit gleicher GesamtoberflŠche.
Die OberflŠche des Tetraeders besteht aus vier gleichseitigen Dreiecken, jene des Oktaeders aus acht gleichseitigen Dreiecken. Die Dreiecke des Oktaeders mŸssen also flŠchenmŠ§ig halb so gro§ sein wie jene des Tetraeders.
2 Tetraeder und Oktaeder mit gleicher OberflŠche
Die Abbildung 1 gibt eine GegenŸberstellung.
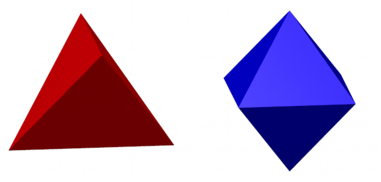
Abb. 1: Die beiden Kšrper haben die gleiche OberflŠche
Die Abbildung 2 gibt die Durchdringung der beiden Kšrper. Ebenfalls ist noch ein oberflŠchengleicher WŸrfel beigegeben.
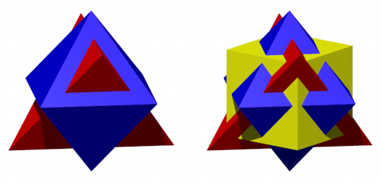
Abb. 2: Durchdringung oberflŠchengleicher Kšrper
3 Dreieck flŠchenmŠ§ig halbieren
Die Abbildung 3 zeigt eine Zerlegung eines Dreiecks in zwei flŠchengleiche Dreiecke.
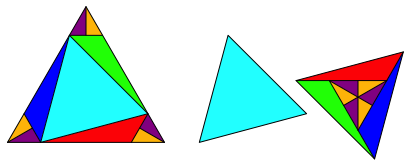
Abb. 3: Dreieck halbieren
4 Abwicklungen
Die Abbildung 4 zeigt einen Vorschlag fŸr die Abwicklungen der beiden Kšrper.
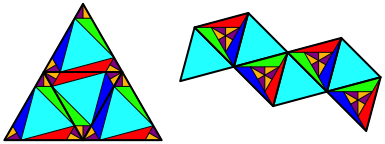
Abb. 4: Abwicklungen
5 Modelle
Die Abbildung 5 zeigt den Tetraeder. Es liegt auf einer SeitenflŠche. Je gegenŸberliegende Kanten haben dieselbe Farbe.
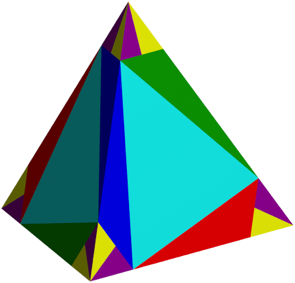
Abb. 5: Tetraeder
Die Abbildung 6 zeigt das Oktaeder. Es liegt auf einer SeitenflŠche. Je gleichfarbige Kanten bilden ein Quadrat.
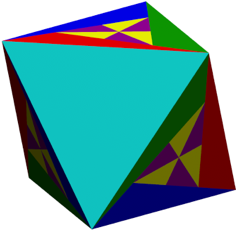
Abb. 6: Oktaeder
Weblinks
Hans Walser: Dreieck halbieren
www.walser-h-m.ch/hans/Miniaturen/D/Dreieck_halbieren/Dreieck_halbieren.htm
Hans Walser: OberflŠchengleiche Tetraeder und WŸrfel
www.walser-h-m.ch/hans/Miniaturen/O/Oberflaechengl_Tetr_Wuerfel/Oberflaechengl_Tetr_Wuerfel.htm
Patrick Wiesner, Homepage