Hans Walser, [20190418]
OberflŠchengleiche Tetraeder und WŸrfel
Anregung: Patrik G. K. Wiesner, BSc ETHZ, Davidgasse 42, A - 1100 Wien
1 Zerlegungsgleichheit
Nach einem Satz von Dehn (1900) sind volumengleiche Tetraeder und WŸrfel nicht zerlegungsgleich.
FlŠchengleiche ebene Polygone sind nach einem Satz von Hilbert aber immer zerlegungsgleich. Wir suchen eine gemeinsame Zerlegung der OberflŠchen von Tetraeder und WŸrfel. Dazu arbeiten wir in den Abwicklungen dieser Kšrper.
2 Tetraeder und WŸrfel
Die Abbildung 1 zeigt eine GegenŸberstellung und eine Durchdringung der beiden Kšrper mit gleicher OberflŠche.
Abb. 1: Tetraeder und WŸrfel mit gleicher OberflŠche
3 FlŠchengleiche Abwicklungen
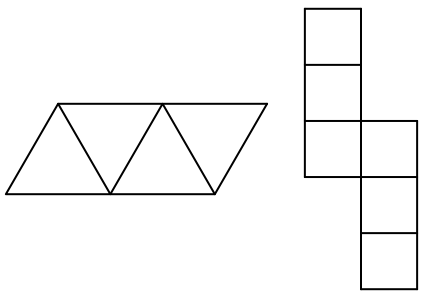
Abb. 2: FlŠchengleiche Abwicklungen
Die Abbildung 2 zeigt exemplarisch je eine Abwicklung von Tetraeder und WŸrfel mit gleicher GesamtflŠche.
4 Zerlegungsgleiche Abwicklungen
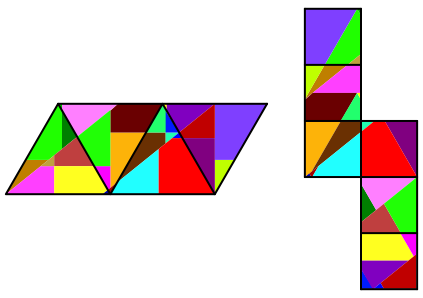
Abb. 3: Zerlegungsgleiche Abwicklungen
In den beiden Zerlegungen der Abbildung 3 haben entsprechende Teile dieselbe Farbe und sind gleich orientiert. Sie kšnnen also durch eine Translation von der einen Abwicklung in die andere gebracht werden. Jedes Teil wird genau einmal verwendet.
Die Abbildung 4 zeigt eine andere Lšsung. Die Teile werden mehrfach verwendet.
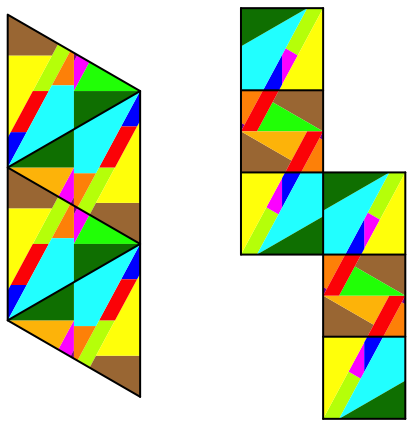
Abb. 4: Andere Lšsung
5 Daten
Wir gehen aus von einem WŸrfel der KantenlŠnge 1. Seine OberflŠche ist daher 6. FŸr die OberflŠche des Tetraeders mit der KantenlŠnge s finden wir:
(1)
Aus S = 6 ergibt sich:
(2)
Weblink
Patrick Wiesner, Homepage