1 Worum geht es?

Optische Täuschungen im Kontext von Quadraten und Spiralen

2 Schiefes Quadrat?

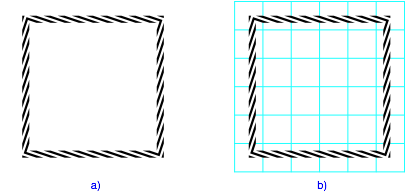
Abb. 1: Schiefes Quadrat?

Wir haben den Eindruck, das Quadrat (Abb. 1) sei schief in den Text eingefügt worden. Sogar bei Hinterlegung eines Quadratrasters behalten wir diesen Eindruck bei.

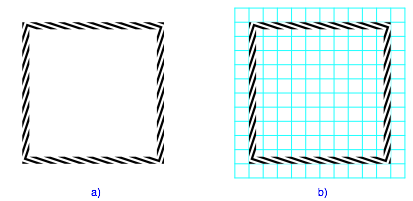
Abb. 2: Verfeinertes Raster

Erst bei der Verfeinerung des Rasters (Abb. 2b) geben wir widerwillig klein bei.

Die optischen Effekte ergeben sich durch die schräge schwarz-weiße Binnenstruktur. Das Phänomen wird als Zöllner-Täuschung (Karl Friedrich Zöllner, 1834-1882) bezeichnet.

3 Eckige Spirale?

Wenn man sich auf das Zentrum der Abbildung 3 konzentriert, könnte man sogar zur Vermutung gelangen, dass sich da nicht verschiedene Quadrate befinden, sondern eine eckige Spirale. Dies besonders dann, wenn der Rand nicht so offensichtlich ist, etwa in einem Ausschnitt aus der um 45° gedrehten Figur (Abb. 3b).

Abb. 3: Spirale?

Die Abbildung 4 zeigt eine echte eckige Spirale.

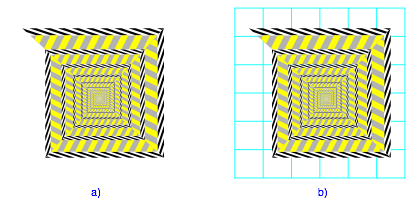
Abb. 4: Spirale

Auch hier haben wir den (falschen) Eindruck, die Figur sei schief in den Text eingebettet.

4 Spirale?

Abb. 5: Spirale?

Figuren dieser Art wurden erstmals 1908 vom britischen Psychologen James Fraser beschrieben. Sie sehen aus wie logarithmische Spiralen, bestehen aber aus einer Folge von Kreisen. Dies wird sofort einsichtig, wenn das Bild nicht rechteckig beschnitten wird (Abb. 6).

Abb. 6: Äußerster Kreis nachvollziehbar

Websites

Hans Walser: Optische Täuschungen

http://www.walser-h-m.ch/hans/Miniaturen/O/Opt_Taeuschung/Opt_Taeuschung.htm

Hans Walser: Optische Täuschungen mit Sinuskurven

www.walser-h-m.ch/hans/Miniaturen/O/Opt_Taeuschung3/Opt_Taeuschung3.htm