Hans Walser, [20181219]

Orgelpfeifen

1 Worum geht es?

Abb. 1: Orgelprospekt

Die Abbildung 1 zeigt den Orgelprospekt der St.-Nikolai-Kirche Grünlichtenberg (1866/67). In der Mittelachse und den beiden Außenachsen sind die Pfeifen so angeordnet, dass in der Mitte die längste Pfeife steht. In den Zwischenachsen sehen wir ein monotones Wachstum der Pfeifenlängen.

Dies wirft folgendes Problem auf: Gegeben sei eine monoton wachsende Folge. Gesucht ist eine Veränderung der Reihenfolge derart, dass das größte Folgenglied möglichst in die Mitte zu liegen kommt und es auf beiden Seiten abwärts geht.

2 Bearbeitung

Wir beginnen mit einer monoton wachsenden endlichen Folge:

(1)

Gesucht ist eine Veränderung der Reihenfolge derart, dass möglichst in die Mitte zu liegen kommt. Weiter soll das kleinste Folgenglied links bleiben, das zweitkleinste Folgenglied soll an die letzte Stelle zu liegen kommen, das drittkleinste Folgenglied neu an zweiter Stelle links und so weiter. Diese Festlegung hat eine Paritätsunterscheidung zur Folge: Bei einer ungeraden Anzahl von Folgengliedern ist dann das größte Folgenglied in der Mitte und das zweitgrößte rechts davon. Bei einer geraden Anzahl von Folgengliedern gibt es kein mittleres Glied. In der Mitte stehen links das zweitgrößte und rechts das größte Folgenglied.

2.1 Indextransformation

Wir bezeichnen mit j den Laufindex der Folge (1) und mit den Index desjenigen Folgengliedes von (1), das nach der Veränderung der Reihenfolge an der Stelle j liegt.

Das Problem wird gelöst durch folgende Veränderung der Reihenfolge:

(2)

Die Idee ist, das Maximum in die Mitte zu setzen und von daher auf beide Seiten hinunterzugehen.

2.2 Indexbeispiele

In der Tabelle 1 ist m = 3 und n = 9.

j	k
3	3
4	5
5	7
6	9
7	8
8	6
9	4

Tab. 1: Beispiel

Wir können natürlich auch mit dem Index null beginnen (Tab. 2).

j	k
0	0
1	2
2	4
3	5
4	3
5	1

Tab. 2: Beispiel

Die Sache funktioniert auch mit negativen Indizes (Tab. 3).

j	k
–7	–7
–6	–5
–5	–3
–4	–1
–3	1
–2	0
–1	–2
0	–4
1	–6

Tab. 3: Beispiel

3 Lineares Wachstum

In der Abbildung 2 wird die Reihenfolge einer linearen Folge verändert.

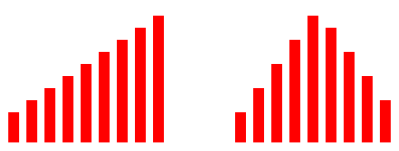
Abb. 2: Lineares Wachstum

Bei der veränderten Reihenfolge ist die Symmetrie an der Spitze etwas gestört (Abb. 3).

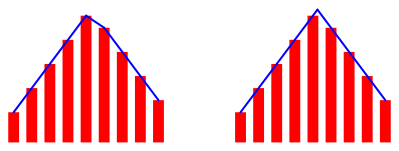
Abb. 3: Gestörte Symmetrie

Die geometrische Spitze liegt etwas rechts von der Mitte. Dies erklärt den merkwürdigen Summanden in (2).

Die eine Seite passt nach dem Spiegeln in die Zwischenräume der anderen Seite. Dies ist die sogenannte Reißverschlusssymmetrie (Abb. 4).

Abb. 4: Reißverschlusssymmetrie

4 Exponentielles Wachstum

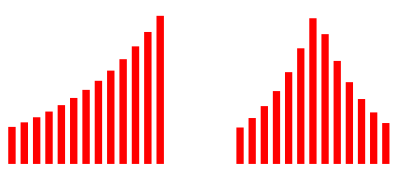
Abb. 5: Exponentielles Wachstum

In der veränderten Reihenfolge ist die Spitze wiederum leicht rechts vom Maximum.

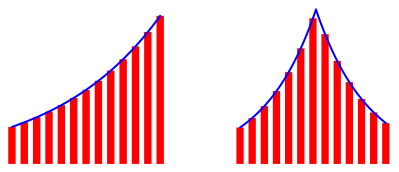
Abb. 6: Exponentialkurven

Die Abbildung 7 zeigt einen entsprechenden Orgelprospekt (Dom zu Salzburg). Allerdings nimmt hier auch der Durchmesser der Orgelpfeifen zu.

Abb. 7: Dom zu Salzburg

5 Sinusoidales Wachstum

Wir arbeiten mit der Folge (Abb. 8):

(3)

Man beachte, dass das erste Folgenglied den Wert null hat.

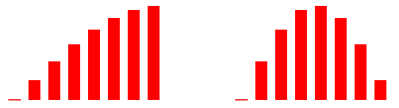
Abb. 8: Sinusoidale Folge

Die Umrisskurven sind Sinuskurven, ohne Spitze.

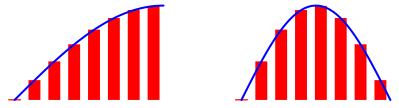
Abb. 9: Sinuskurven

Wir verändern jetzt die Folge scheinbar geringfügig:

(4)

Im Staffelbild ist der Unterschied von Auge nicht wahrnehmbar (Abb. 10).

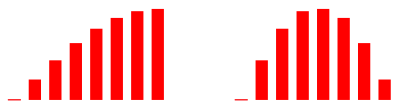
Abb. 10: Leicht geänderte Folge

Die Umrisskurve ist in der veränderten Reihenfolge nicht mehr eine durchgehende Sinuskurve, sondern hat eine Spitze nach unten (Abb. 11).

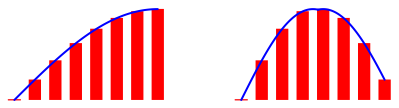
Abb. 11: Spitze nach unten

Websites

Hans Walser: Trigonometrische Identität

http://www.walser-h-m.ch/hans/Miniaturen/T/Trigo_Id/Trigo_Id.htm