Hans Walser, [20231128]
Origami-Oktaeder
1 Worum es geht
Oktaeder aus acht Bauteilen, welche je aus einem Origami-Dreieck gefaltet werden.
2 Das Modell
Die Abbildung 1 zeigt das Origami-Oktaeder.

Abb. 1: Origami-Oktaeder
Es besteht aus zweimal vier Bauteilen, vorzugsweise in zwei verschiedenen Farben. Die Bauteile in den beiden Vierer-Gruppen sind unterschiedlich. Es gibt vier Schlitz-Teile (hellblau in Abb. 1) und vier Laschen-Teile (magenta in Abb. 1).
3 Faltvorgang
Alle Bauteile werden aus gleich großen dreieckigen Origami-Papieren gefaltet. Der Faltvorgang ist aber bei den beiden Vierer-Gruppen unterschiedlich.
3.1 Schlitz-Teil
Die Abbildung 2 zeigt das Start-Dreieck für einen Schlitz-Teil.
Die roten Faltlinien sind Talfalten, die blauen Bergfalten. Das Bauteil wird aus der Sicht von innen (bezogen auf das fertige Modell) dargestellt.
Zuerst werden die drei Symmetrieachsen des Dreiecks gefaltet und wieder zurückgefaltet.
Dann werden die Ecken auf die gegenüberliegenden Seitenmitten gefaltet und wieder zurückgefaltet. Dies ergibt das zentrale rote Teildreieck.
Schließlich werden in den drei äußeren Teildreiecken je eine Symmetrieachse als Bergfalten gefaltet. Dazu muss das Papier gewendet werden. Die drei blauen Faltlinien sind zyklisch angeordnet, sie werden durch Dritteldrehungen des Origami-Papiers aufeinander abgebildet.
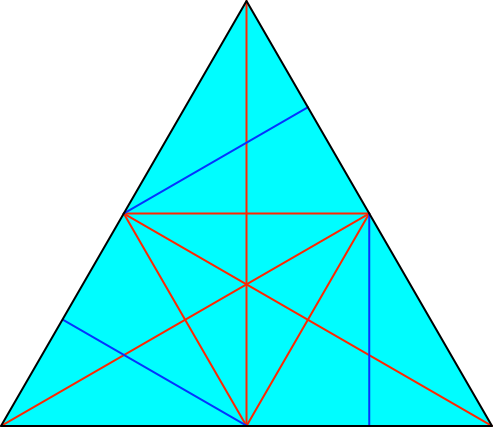
Abb. 2: Start-Dreieck für Schlitz-Teil
In der Abbildung 3 sind die gefalteten Außendreiecke an den Bergfalten leicht angehoben. Aus diesen Außendreiecken werden die Einschiebeschlitze des Bauteils gemacht.
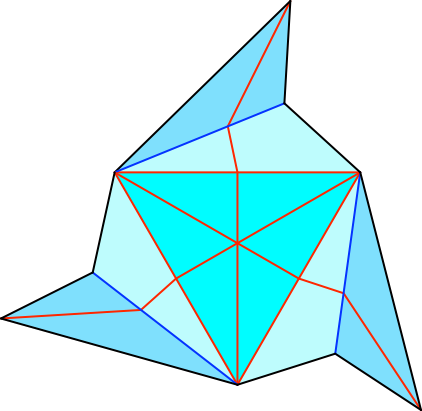
Abb. 3: Angehobene Außendreiecke
Die Abbildung 4 und 5 zeigen das Falten eines Einschiebeschlitzes.
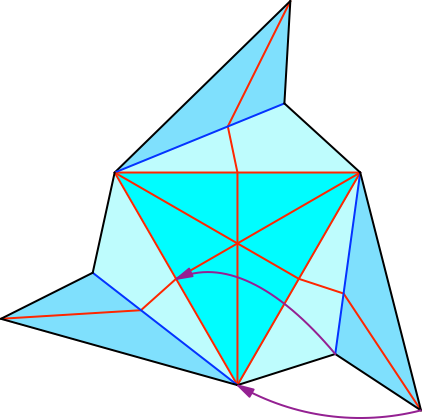
Abb. 4: Einschiebeschlitz falten
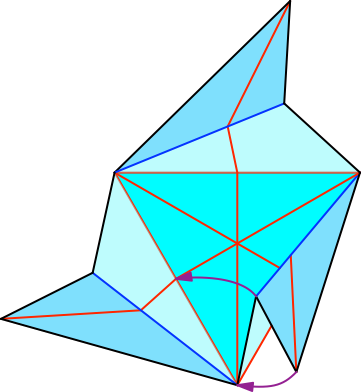
Abb. 5: Einschiebeschlitz falten, Zwischenstufe
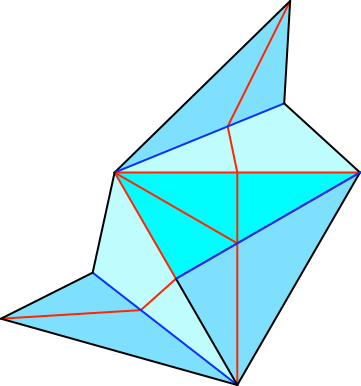
Abb. 6: Erster Einschiebeschlitz
Der Einschiebschlitz befindet sich an der Außenkante rechts unten in der Abbildung 6.
Die Tasche des analog gefalteten zweiten Einschiebeschlitzes (Abb. 7) befindet sich über dem dicken Ende der ersten Tasche.
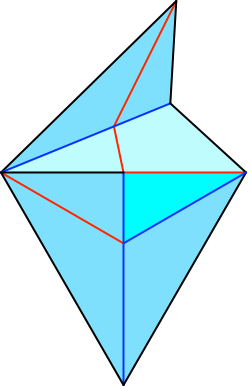
Abb. 7: Zweiter Einschiebeschlitz
Die Tasche des dritten Einschiebeschlitzes (Abb. 8) ist einerseits über dem dicken Ende des zweiten, andererseits mit seinem dicken Ende unter dem spitzen Ende der ersten Tasche.
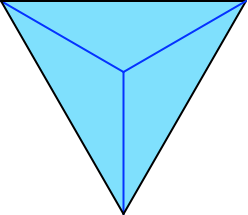
Abb. 8: Dritter Einschiebeschlitz
Es entsteht eine zyklische Überlappungsordnung (Abb. 9). Das Einschieben des dicken Endes der dritten Tasche unter das spitze Ende der ersten erfolgt mit Hilfe eines flachen Gerätes, zum Beispiel einem Brieföffner oder der Klinge eines Taschenmessers.

Abb. 9: Schlitz-Teil
3.2 Laschen-Teil
Die Abbildung 10 zeigt die Ausgangslage für den Laschen-Teil. Alle Faltlinien sind Talfalten.
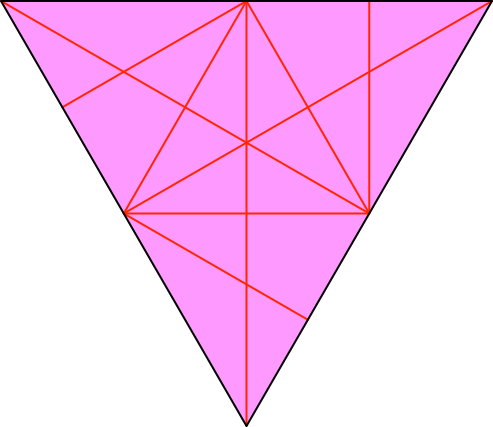
Abb. 10: Laschenteil
Die Abbildungen 11 und 12 zeigen das Falten der Einstecklaschen.
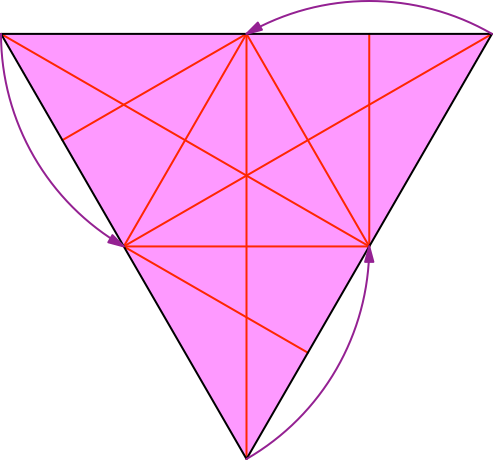
Abb. 11: Falten der Einstecklaschen
Bei den fertigen Einstecklaschen (Abb. 12) ist nun die andere Papierseite sichtbar. Daher sind die Faltlinien dort als Bergfalten gezeichnet.
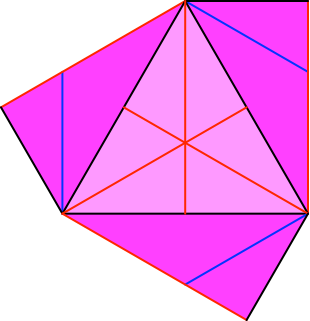
Abb. 12: Einstecklaschen
4 Zusammenbau
Die Abbildung 13 zeigt das Einschieben einer Einstecklasche in einen Einschiebeschlitz. Zur Verdeutlichung ist die Einschiebetasche transparent gezeichnet.
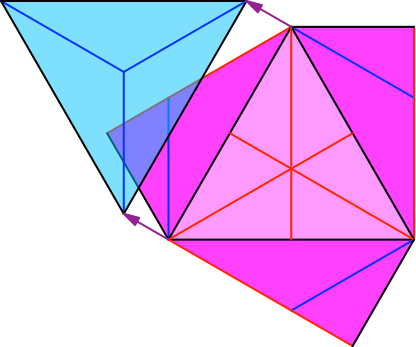
Abb. 13: Einschieben
In den Abbildungen 14 und 15 sind ein Schlitz-Teil und ein Laschen-Teil zusammengeschoben.
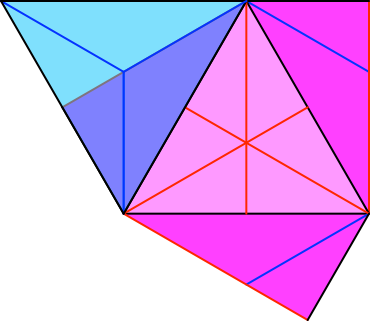
Abb. 14: Eingeschoben

Abb. 15: Eingeschoben am realen Modell
Die Abbildungen 16 und 17 zeigen eine Auslegeordnung mit den vier Schlitz-Teilen und drei Laschen-Teilen. Bis auf das noch fehlende vierte Laschen-Teil ist dies eine Abwicklung („Netz“) des Oktaeders.
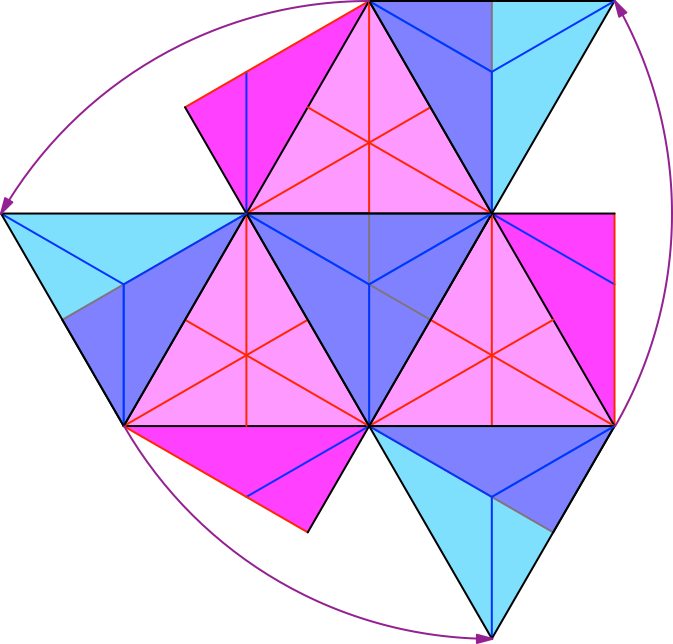
Abb. 16: Vier Schlitz-Teile und drei Laschen-Teile

Abb. 17: Reales Modell
Das zentrale Schlitz-Teil wird zum Boden des als Antiprismas gedachten Oktaeders. Die übrigen Teile klappen wir hoch und schieben die freistehenden Laschen ein.
Schließlich wird noch das vierte Laschen-Teil von oben her eingebaut. Es entsteht das Modell der Abbildung 1.
5 Ausblick
Beim Tetraeder (Abb. 18) kann die Oberfläche nicht in zwei Klassen von je zwei Schlitz-Teilen und zwei Laschen-Teilen getrennt werden.
Hingegen ist es zum Beispiel möglich, einen reinen Schlitz-Teil als „Boden“ zu verwenden (hellblaues Teil in Abb. 18) und die drei übrigen Teile mit je einem Schlitz und zwei Laschen zu gestalten.

Abb. 18: Tetraeder
Das Ikosaeder habe ich nicht ausprobiert. Es müsste auch mit gemischten Teilen gearbeitet werden. Es ist zu befürchten, dass die Laschen wegen dem großen Diederwinkel nicht gut in den Einschiebetaschen halten.
Weblinks
Hans Walser: Origami-Dreieck
https://walser-h-m.ch/hans/Miniaturen/D/Dreieck-Origami/Dreieck-Origami.htm