Hans Walser, [20180331]
Origami-RŠtsel
1 Faltvorgang
Am linken Rand bringen wir in der Mitte eine Faltmarkierung an (rot in Abb. 1a). Dann falten wir so, dass die untere Kante auf diese Markierung und die rechte untere Ecke auf die Oberkante zu liegen kommen (Abb. 1b).
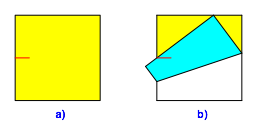
Abb. 1: Erster Faltschritt
Beim Berźhrungspunkt auf der Oberkante bringen wir eine zweite Faltmarkierung an (blau in Abb. 2a) und falten auf (Abb. 2b).
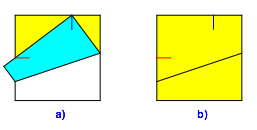
Abb. 2: Markieren und Auffalten
Nun falten wir weiter gemŠ§ Abbildung 3a. Wie gro§ ist der in der Abbildung 3b eingezeichnete Winkel?
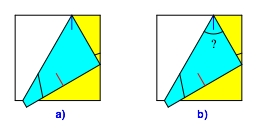
Abb. 3: Zweiter Faltschritt
2 Bearbeitung
Der Winkel misst 60ˇ. Dies kann wie folgt eingesehen werden. Wir setzen die KantenlŠnge des Origamipapiers auf 1 und arbeiten mit den Daten und Bezeichnungen der Abbildung 4.
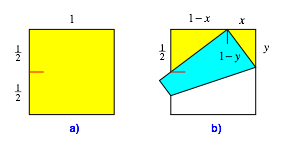
Abb. 4: Daten und Bezeichnungen
Aus der €hnlichkeit der beiden gelben rechtwinkligen Dreiecke (Abb. 4) folgt:
![]() (1)
(1)
Der Satz des Pythagoras ergibt fźr das Dreieck rechts oben:
![]() (2)
(2)
Gleichsetzen von (1) und (2) liefert die quadratische Gleichung fźr x:
![]() (3)
(3)
Diese Gleichung (3) hat die beiden Lšsungen:
![]() (4)
(4)
Die zweite Lšsung ist die fźr uns relevante Lšsung (was ist mit der ersten Lšsung?). Fźr den zweiten Faltschritt (Abb. 3) haben wir somit die Ma§verhŠltnisse der Abbildung 5.
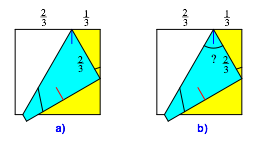
Abb. 5: Ma§e
Das gelbe rechtwinklige Dreieck rechts oben ist ein halbes gleichseitiges Dreieck. Daraus ergibt sich, dass die drei Winkel bei der blauen Faltmarkierung alle 60ˇ messen.
3 Erinnerung
Die Abbildung 6 zeigt eine konventionelle Methode, einen Winkel von 60ˇ mit Falten zu konstruieren.

Abb. 6: Falten eines Winkels von 60ˇ