Hans Walser, [20140901]
Origami im Raum
Anregung: G. G., B.
1 Worum geht es?
Statt mit einem quadratischen Origami-Papier arbeiten wir mit entsprechenden Analoga im Raum.
2 Klassisches Origami und einige Beispiele
Das klassische Origami verwendet ein quadratisches Papier, das dann gefaltet wird. Papier wird in der Regel als zweidimensional gesehen obwohl es wegen seiner Dicke streng genommen ein dreidimensionales Objekt ist. Das Falten bentigt auf den dreidimensionalen Umgebungsraum. Wenn wir aber nur an den Resultaten interessiert sind, knnen wir abstrakt von zweidimensionaler Geometrie sprechen. Im Folgenden einige einfache Beispiele.
2.1 Kantenmitten einfalten
Mit Hilfe der Diagonalen oder der Mittelparallelen bestimmen wir zunchst den Mittelpunkt. Dann falten wir die Kantenmitten in den Mittelpunkt des Quadrates (Abb. 1).

Abb. 1: Einfalten der Kantenmitten
Es entsteht ein vierfach berlagertes Quadrat. Der Flcheninhalt ist ein Viertel des Flcheninhaltes des Origami-Quadrates. Der Umriss des neuen Quadrates liegt auf den Mittelsenkrechten der Kantenmitten und des Mittelpunktes.
Man beachte die ãPropellerfaltungÒ im letzten Schritt. Sie ist rein sthetisch begrndet und soll eine vierteilige zyklische Symmetrie ermglichen.
2.2 Ecken einfalten
Wir falten die Ecken in die Mitte (Abb. 2).
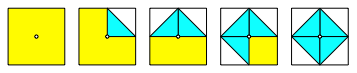
Abb. 2: Ecken einfalten
Es entsteht ein doppelt berlagertes Quadrat. Der Flcheninhalt des neuen Quadrates ist demzufolge die Hlfte des Flcheninhaltes des Origami-Quadrates. Der Umriss des neuen Quadrates liegt auf den Mittelsenkrechten der Endpunkte und des Mittelpunktes.
2.3 Wie es auch noch geht
Wir falten exemplarisch ãDrittelpunkteÒ auf den Kanten in die Mitte (Abb. 3).

Abb. 3: Einfalten der Drittelpunkte in die Mitte
Es
entsteht wieder ein Quadrat. Der Umriss des neuen Quadrates liegt auf den Mittelsenkrechten
der Drittelpunkte und des Mittelpunktes. Die berlagerung ist nicht mehr homogen. Der Flcheninhalt
des neuen Quadrates ist ![]() des
Flcheninhaltes des Origami-Quadrates.
des
Flcheninhaltes des Origami-Quadrates.
Allgemein
Erhalten wir in der Situation der Abbildung 4 einen Flcheninhalt von ![]() des
Flcheninhaltes des Origami-Quadrates. Die berlagerung ist im Allgemeinen
nicht homogen.
des
Flcheninhaltes des Origami-Quadrates. Die berlagerung ist im Allgemeinen
nicht homogen.
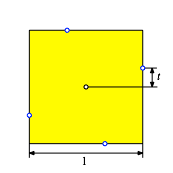
Abb. 4: Allgemeiner Fall
3 Kubisches Origami
Wir denken uns einen Wrfel als Origami-Ausgangsmaterial. Zum Falten mssten wir in die vierte Dimension ausweichen. Wir knnen uns aber auch mit einem Schnitt mit der Mittelnormalebene zweier aufeinander zu faltender Punkte behelfen. Leider knnen wir nicht mehr wie bei den Abbildungen 1 bis 3 mit verschiedenen Farben fr Vorderseite und Rckseite operieren, da die Begriffe vorn und hinten sich auf die vierte Dimension beziehen mssten.
3.1 Seitenmitten einfalten
Wir falten die Mittelunkte der sechs Seitenflchen des Wrfels in den Wrfelmittelpunkt. Dadurch einsteht ein achtfach berlagerter Wrfel. Die Abbildung 5 zeigt die ersten Faltschritte und das Endresultat.
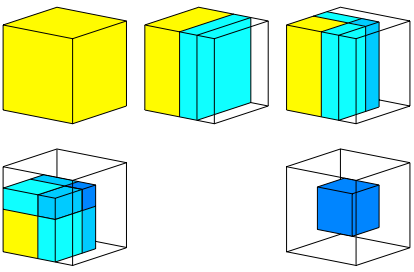
Abb. 5: Seitenmitten in Wrfelmitte einfalten
3.2 Kantenmitten einfalten
Die Abbildung 6 zeigt die ersten Schritte und das Endresultat beim Einfalten der Kantenmitten.
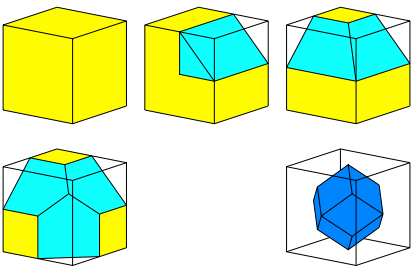
Abb. 6: Kantenmitten in Wrfelmitte einfalten
Es entsteht ein Rhombendodekaeder. Sein Volumen ist ein Viertel des Volumens des Origami-Quaders.
Die berlagerung ist nicht homogen.
3.3 Ecken einfalten
Das ist das spannendste Beispiel. Die Abbildung 7 zeigt das Einfalten der ersten Ecke in die Wrfelmitte als transparentes Bild.
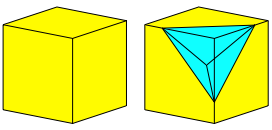
Abb. 7: Einfalten einer Ecke
Die Abbildung 8 zeigt das Endresultat. Es handelt sich um ein abgestumpftes Oktaeder.
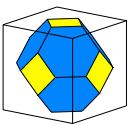
Abb. 8: Abgestumpftes Oktaeder
Das Volumen des abgestumpften Oktaeders ist die Hlfte des Volumens des Origami-Quaders.
3.4 Raumfller
Die drei Ergebnisse unserer Faltprozesse beim Origami-Wrfel also Wrfel, Rhombendodekaeder und abgestumpftes Oktaeder sind so genannte Raumfller. Der Raum kann damit lckenlos und berlappungsfrei ausgefllt werden. Die Abbildungen 9, 10 und 11 zeigen je eine mit diesen Raumfllern aufgeschichtete Pyramide.
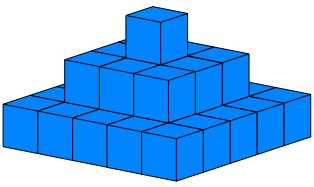
Abb. 9: Wrfelpyramide
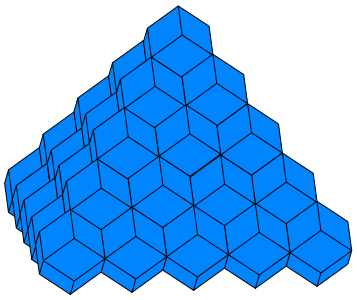
Abb. 10: Pyramide aus Rhombendodekaedern
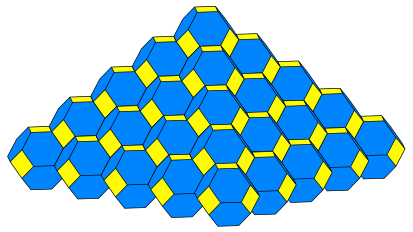
Abb. 11: Pyramide aus abgestumpften Oktaedern
4 Oktaeder-Origami
Oft wird nur der Wrfel als rumliches Analogon des Quadrates gesehen. Das ist eine eingeschrnkte Sicht. Wenn wir das Quadrat als konvexe Hlle von zwei gleich langen sich mittig orthogonal schneidenden Strecken sehen, ist das dreidimensionale Analogon das Oktaeder (Abb. 12).
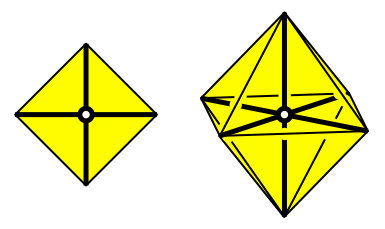
Abb. 12: Quadrat und Oktaeder
Wir arbeiten daher nun mit einem Oktaeder-Origami.
4.1 Seitenmitten einfalten
Es entsteht wieder ein Oktaeder.
4.2 Kantenmitten einfalten
Es entsteht das Rhombendodekaeder.
4.3 Ecken einfalten
Es entsteht ein Wrfel.
4.4 Wie es auch noch geht
Analog zur Abbildung 3 dritteln wir die Oktaederkanten (Abb. 13). Dabei machen wir das so, dass die Kantenabschnitte von einer Oktaederecke aus gesehen abwechslungsweise ein Drittel und zwei Drittel ausmachen. Dies ist in der Abbildung 13 durch die Farbgebung angedeutet.
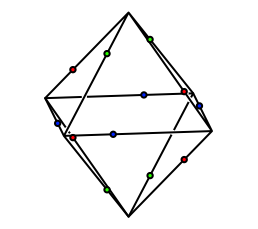
Abb. 13: Dritteln der Oktaederkanten
Wenn wir nun diese Teilpunkte in die Oktaedermitte einfalten, entsteht ein Pentagondodekaeder (Abb. 14). Die Farbgebung richtet sich nach der Farbe der eingefalteten Teilpunkte.
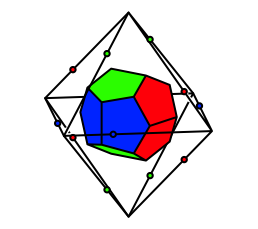
Abb. 14: Dodekaeder
Das Dodekaeder besteht aus zwlf kongruenten, aber nicht regelm§igen Fnfecken. Die Fnfecke sind achsensymmetrisch. Vier der fnf Kanten sind gleich lang. Die fnfte Kante (ãBasisÒ) hat eine abweichende Lnge. An einer Basis sto§en jeweils gleichfarbene Fnfecke zusammen.
Der Winkel α zwischen zwei an einer Basis zusammensto§enden Fnfecken betrgt:
![]()
Allgemein ergibt sich fr Teilpunkte zum Verhltnis a:b (a > b) der Winkel α:
![]()
Wenn wir speziell mit Teilpunkten im Verhltnis des Goldenen Schnittes arbeiten ergibt sich das regelm§ige Pentagondodekaeder.