Hans Walser, [20160615]

Orthodiagonale Vierecke

Anregung: Heinz Klaus Strick, Leverkusen

1 Worum geht es

Orthodiagonale Vierecke haben orthogonale Diagonalen.

In der üblichen Bezeichnung (Abb. 2) können orthodiagonale Vierecke charakterisiert werden durch:

(1)

Die alternierende Seitenquadratsumme ist null.

Es wird versucht, diesen Sachverhalt auf verschiedene Weisen zu illustrieren.

Dazu wird (1) in der Form:

(2)

verwendet (Abb. 1).

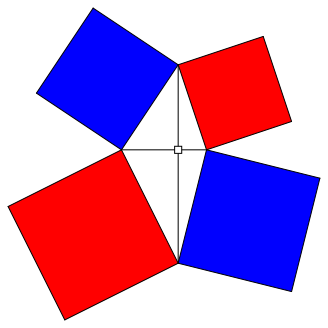
Abb. 1: Rot = Blau

2 Rechnerisches Vorgehen

Für das rechnerische Vorgehen verwenden wir die Bezeichnungen gemäß Abbildung 2.

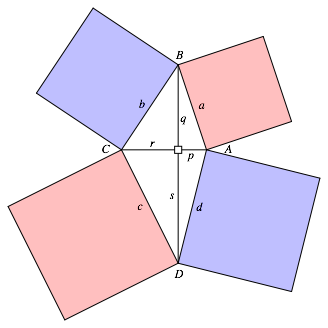
Abb. 2: Bezeichnungen

Nach dem Satz von Pythagoras ist:

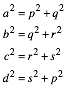(3)

Alternierende Addition in (3) ergibt (1). Wenn die Diagonalen nicht orthogonal sind, ist entweder rot < blau oder rot > blau. Daher die Charakterisierung.

Diese rechnerische Lösung kann auch visualisiert werden. Die Abbildung 3 zeigt für das grüne rechtwinklige Dreieck die Überlagerung der beiden Kathetenquadrate und des Hypotenusenquadrates.

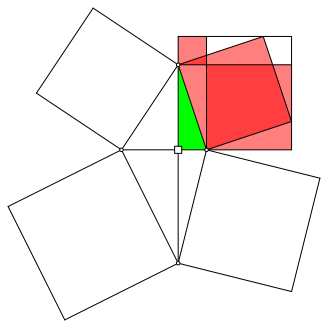
Abb. 3: Visualisierung des Satzes von Pythagoras

In der Abbildung 4 sind entsprechend für alle vier rechtwinkligen Teildreiecke unseres orthodiagonalen Viereckes die Kathetenquadrate eingetragen, wobei aber die Hypotenusenquadrate weggelassen wurden. Offensichtlich ist nun rot = blau.

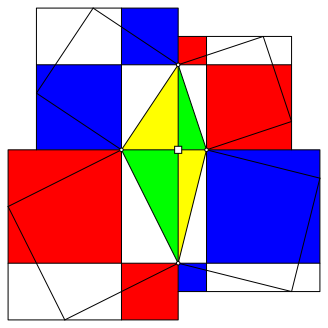
Abb. 4: Rot = blau

3 Zerlegungsbeweise nach Perigal

Die folgenden Zerlegungsbeweise gehen auf Henry Perigal (1801-1898) zurück. Es sind „Schaufelrad-Beweise“.

Für die Zerlegungsbeweise ist eine etwas mühsame Fallunterscheidung gemäß der größenmäßigen Anordnung der Diagonalenabschnitte p, q, r, s erforderlich.

Zunächst nehmen wir an, dass alle Diagonalenabschnitte verschieden lang sind.

Wir bezeichnen den kürzesten Diagonalenabschnitt mit p (piccolo).

(i) r ist der zweitkleinste Diagonalenabschnitt. Dann sind q und s die beiden größten Diagonalenabschnitte. Diese beiden Unterfälle sind überlegungsmäßig symmetrisch.

(ii) r ist der zweitgrößte Diagonalenabschnitt

(iii) r ist der größte Diagonalenabschnitt

Falls gleich lange Diagonalenabschnitte vorhanden sind, ergeben sich Sonderfälle. Bei drei oder vier gleich Langen Diagonalenabschnitten haben wir ein Drachenviereck oder im Sonderfall ein Quadrat. Da ist keine Zerlegung mehr erforderlich. Falls zwei gleich lange Diagonalenabschnitte auf derselben Diagonalen liegen, haben wir ebenfalls ein Drachenviereck. Noch offen sind somit die Fälle, wo zwei gleich lange Diagonalenabschnitte orthogonal sind.

(I) Die beiden gleich langen Diagonalenabschnitte sind kürzer als die beiden anderen

(II) Die beiden gleich langen Diagonalenabschnitte liegen längenmäßig zwischen den beiden anderen

(III) Die beiden gleich langen Diagonalenabschnitte sind länger als die beiden anderen

(IV) Wir haben zwei mal zwei gleich lange Diagonalenabschnitte

Im Folgenden Beispiele.

3.1 Fall (i)

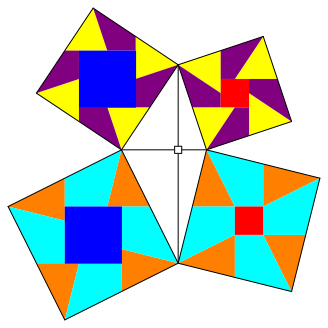
Abb. 5: Fall (i)

Wir sehen sehr schöne die „Schaufelräder“.

Wir haben einen kleinen optischen Täuschungseffekt. Das rote und das blaue Quadrat in der oberen Bildhälfte der Abbildung 5 scheinen größer zu sein als die entsprechenden Quadrate in der unteren Bildhälfte. Sie sind aber je gleich groß. Vor allem beim roten Quadrat ist der Effekt stark. Das hängt damit zusammen, dass das „Umfeld“ in der unteren Bildhälfte größer ist und das zentrale Quadrat daher kleiner erscheinen lässt.

Die Abbildung 6 zeigt den Übergang vom einen Quadratpaar zum anderen. Die zentralen Quadrate (blau und rot) werden vertikal, die Schaufelräder horizontal verschoben.

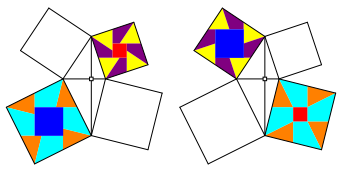
Abb. 6: Flächengleichheit

3.2 Fall (ii)

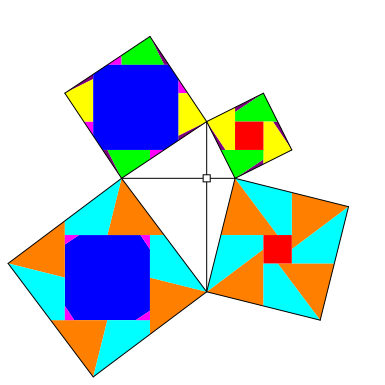
Abb. 7: Fall (ii)

Das blaue zentrale Quadrat ist leicht angeknabbert.

3.3 Fall (iii)

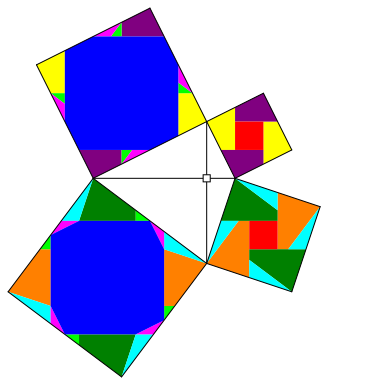
Abb. 8: Fall (iii)

3.4 Fall (I)

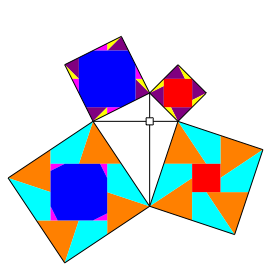
Abb. 9: Fall (I)

3.5 Fall (II)

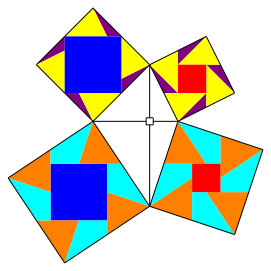
Abb. 10: Fall (II)

3.6 Fall (III)

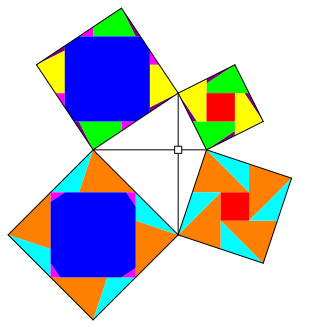
Abb. 11: Fall (III)

3.7 Fall (IV)

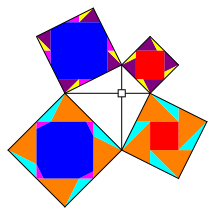
Abb. 12: Fall (IV)

Obwohl der Umriss der Gesamtfigur symmetrisch ist, sind es die Zerlegungen nicht.

4 Beweis mit Flächenverwandlungen nach Euklid

Wir verwenden die Gedankengänge von Euklid (Euklid 1980, S. 32, Erstes Buch, §47).

Wir zerlegen die Quadrate der Abbildung 1 in Rechtecke (Abb. 13).

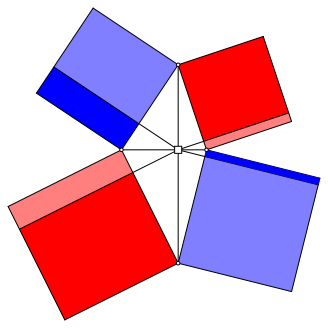
Abb. 13: Zerlegung in Rechtecke

Wir zeigen nun, dass jeweils zwei komplementär gefärbte und komplementär getönte Rechtecke mit gemeinsamer Ecke den gleichen Flächeninhalt haben. Beispiel: Das fette rote Rechteck unten links ist flächengleich zum mageren blauen Rechteck rechts unten.

Dazu verwandeln wir die Rechtecke in flächengleiche Parallelogramme gemäß Abbildung 14.

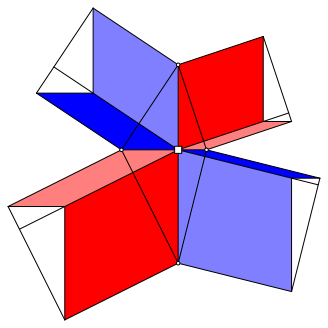
Abb. 14: Parallelogramme

Je zwei komplementäre gefärbte und komplementär getönte Parallelogramme haben eine gemeinsame Grundlinie. Diese ist eine der vier Diagonalenabschnitte.

Aus der Quadrateinbettung gemäß Abbildung 15 geht hervor, dass zwei Parallelogramme mit gemeinsamer Grundlinie auch gleiche Höhen haben, und zwar ebenfalls den Diagonalenabschnitt.

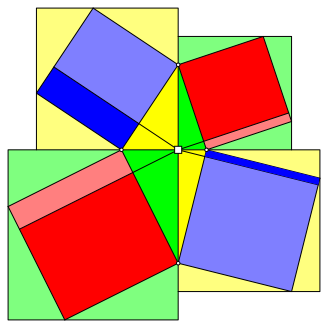
Abb.15: Einbettung in Quadrate

Wir können also die Parallelogramme der Abbildung 12 in vier Paare von kongruenten Quadraten verwandeln (Abb. 16). Damit ist rot = blau bewiesen.

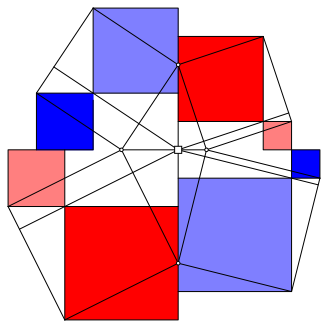
Abb. 16: Rot = Blau

Die Abbildung 16 ist verwandt mit der Abbildung 4.

5 Link mit dem Satz des Pythagoras

Wir lassen in einem orthodiagonalen Viereck eine Seite und damit zwei Diagonalenabschnitte gegen null gehen. Als Grenzlage erhalten wir ein rechtwinkliges Dreieck und die rot = blau – Flächengleichheit ist der Satz des Pythagoras.

Da wir in den Abschnitten 3 und 4 den Satz des Pythagoras nicht verwendet haben, ergeben sich zwei Beweise für diesen Satz des Pythagoras.

6 Ausblick in den Raum

6.1 Orthodiagonales Oktaeder

Ein Polyeder mit drei paarweise orthogonalen Diagonalen durch einen gemeinsamen Punkt ist ein (unregelmäßiges) Oktaeder.

Wir können die achte Seitendreiecke abwechslungsweise rot und blau färben.

Dann ist die Summe der Quadrate der roten Seitenflächen gleich der Summe der Quadrate der blauen Seitenflächen.

Man beachte: „Quadrat einer Seitenfläche“ hat die Dimension vier. Das liegt außerhalb des Vorstellungsraumes des Autors. Bleibt nur noch Rechnen.

6.2 Spezielles Tetraeder

Für den Beweis studieren wir zunächst ein Tetraeder mit drei paarweise orthogonalen Kanten der Längen p, q, r durch eine gemeinsame Ecke (Abb. 17).

Abb. 17: Tetraeder

Die drei paarweise orthogonalen Seitendreiecke des Tetraeders haben die Flächeninhalte:

(4)

Für die Berechnung des Seitendreieckes ABC berechnen wir das Tetraedervolumen auf zwei Arten. Zunächst ist:

(5)

Wir denken uns nun ein Koordinatensystem eingepasst mit dem Ursprung in O so dass:

(6)

Die Ebene ABC hat somit die Gleichung:

(7)

Über die Hessesche Normalform finden wir den Abstand vom Ursprung und damit die auf die Dreiecksfläche ABC bezogene Tetraederhöhe:

(9)

Wir vergleichen nun das Tetraedervolumen

(10)

mit (5) und erhalten:

(11)

Somit ist:

(12)

Wegen (4) heißt das in Worten:

In unserem Tetraeder ist das Quadrat der Seitenfläche ABC gleich der Summe der Quadrate der drei übrigen (paarweise orthogonalen) Seitenflächen.

6.3 Verallgemeinerung des Satzes von Pythagoras

Wir haben somit eine Verallgemeinerung des Satzes von Pythagoras in den Raum. Er operiert allerdings mit vierdimensionalen Begriffen und kann daher nicht visualisiert werden.

6.4 Orthodiagonales Oktaeder

Zurück zu unserem Oktaeder mit drei paarweise orthogonalen Diagonalen durch einen gemeinsamen Punkt. Wir zerlegen dieses Oktaeder mit Hilfe der Diagonalen in acht Tetraeder mit je drei paarweise orthogonalen Kanten, schreiben obigen Satz für jedes Tetraeder auf und addieren rot-blau-alternierend.

So erhalten wir: Die Summe der Quadrate der roten Seitenflächen ist gleich der Summe der Quadrate der blauen Seitenflächen.

Literatur

Euklid (1980): Die Elemente. Nach Heibergs Text aus dem Griechischen übersetzt und herausgegeben von Clemens Thaer. Darmstadt: Wissenschaftliche Buchgesellschaft. ISBN 3-534-01488-X

Websites

Abgerufen 16. 06. 2016

Adrian Christen: Beweise des Satzes von Pythagoras

www.mathematik-nachhilfe.de/wp-content/uploads/Pythagoras.pdf

Martin Josefsson: Characterizations of Orthodiagonal quadrilaterals:

http://forumgeom.fau.edu/FG2012volume12/FG201202.pdf

Hans Walser: Viereck mit orthogonalen Diagonalen

www.walser-h-m.ch/hans/Miniaturen/V/Viereck_m_orth_Diag/Viereck_m_orth_Diag.htm

Hans Walser: Miniaturen Pythagoras

www.walser-h-m.ch/hans/Miniaturen_Uebersicht/Pythagoras/index.html

Hans Walser: Miniaturen Optische Effekte

www.walser-h-m.ch/hans/Miniaturen_Uebersicht/Optische_Effekte/index.html