Hans Walser, [20090120a]
Orthogonale Diagonalen
1
Worum es geht
In
einem Viereck mit den Seiten a, b, c, d sind die Diagonalen genau dann
orthogonal, wenn fźr die Seiten gilt: 
.
2
Beweis mit Kosinussatz
Fźr den Beweis
verwenden wir die Bezeichnungen der Figur.
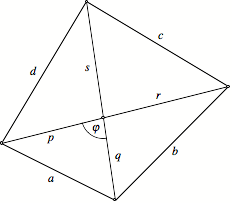
Bezeichnungen
Aus dem Kosinussatz
ergibt sich:
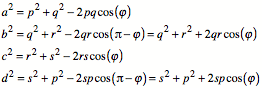
Fźr die alternierende
Quadratsumme folgt daraus:
3
Vektorieller Beweis
Wir verwenden die Seitenvektoren
, 
, 
, 
gemŠ§ Figur.
Ferner seien 
und 
die beiden
Diagonalvektoren.
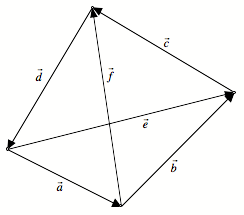
Vektoren
Nun drźcken wir die
Vektoren 
, 
, 
und 
durch die
Vektoren 
, 
und 
aus:
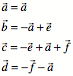
Fźr die Quadrate
erhalten wir:
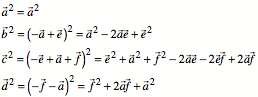
Somit ergibt sich fźr
die alternierende Quadratsumme:
Daraus folgt die
Behauptung.
4
Tetraeder
Der vektorielle Beweis
ist nicht an die Ebene gebunden. Er gilt auch fźr vier Ecken im Raum, also fźr
ein Tetraeder.
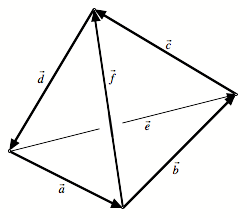
Tetraeder
Bei einem Tetraeder
sind also zwei gegenźberliegende Kanten genau dann orthogonal, wenn die
alternierende Quadratsumme der vier źbrigen Kanten verschwindet.
5 Briefumschlag
Bei einem Viereck mit
orthogonalen Diagonalen lassen sich die Ecken auf den Diagonalenschnittpunkt
einfalten, so dass ein ăBriefumschlagŇ entsteht (unter Weglassung der
Klebefalze).
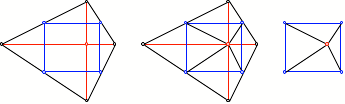
Briefumschlag