1 Worum geht es?

Verallgemeinerung im Umfeld von Ortsbogen und Umfangwinkelsatz

2 Konstruktion

Bei einem Kreisbogen mit Sehne klappen wir den Ergänzungsbogen hinein. Auf der Sehne wählen wir symmetrisch zwei Punkte (Abb. 1a).

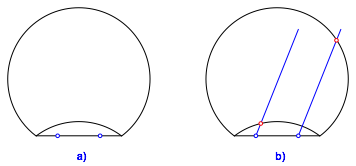
Abb. 1: Symmetrische Punkte und Parallelen

Durch die beiden Punkte legen wir parallele Geraden. Die eine (rechts) schneiden wir mit dem großen Bogen, die andere mit dem kleinen (Abb. 1b).

Wir verbinden die beiden Schnittpunkte (Abb. 2a).

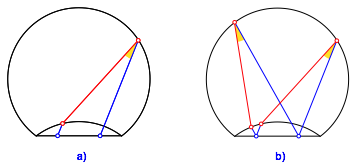
Abb. 2: Invarianter Winkel

So entsteht ein Winkel, der gegenüber Verdrehungen der Parallelen invariant ist (Abb. 2b). Die Animation 1 illustriert den Sachverhalt.

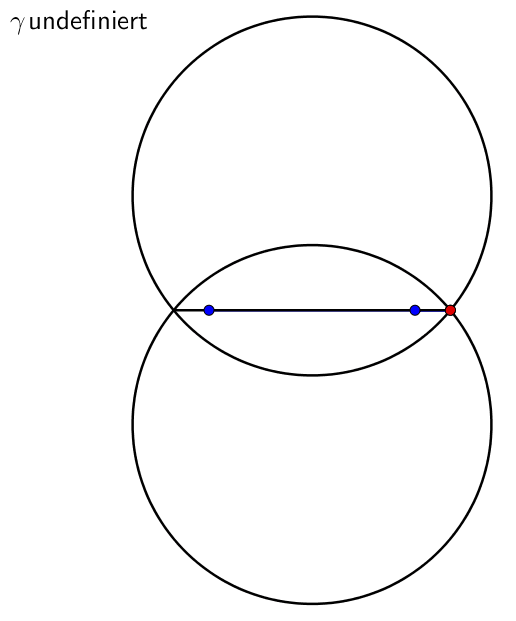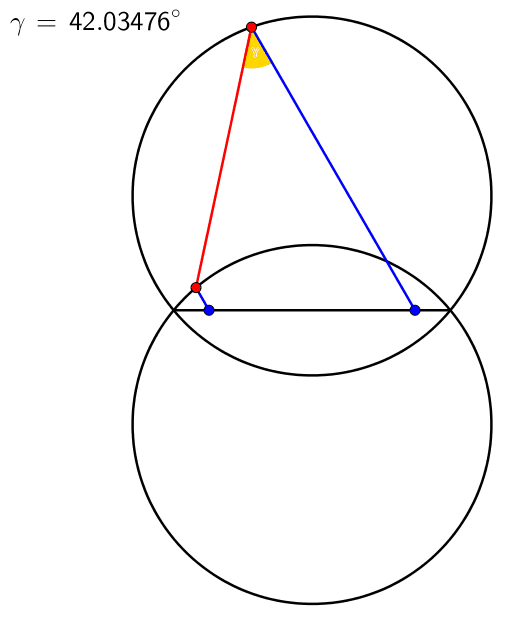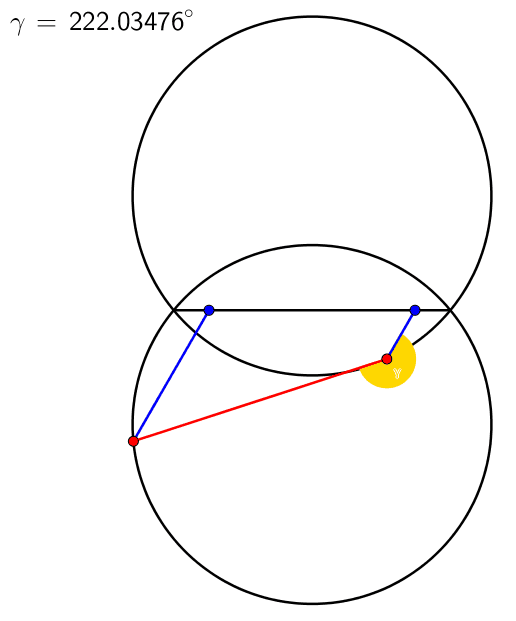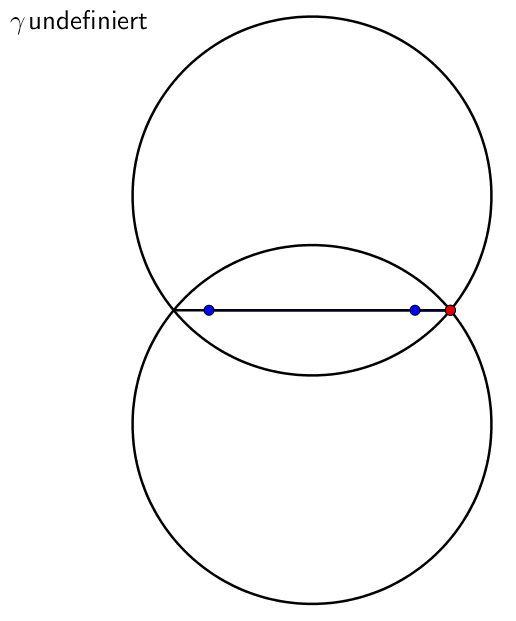
Animation 1: Invarianter Winkel

Bevor wir zum Beweis schreiten, einige Sonderfälle und andere Dispositionen.

3 Sonderfall

Wir setzen die beiden Punkte an die Enden der Sehne (Abb. 3). Dadurch schrumpft der Mechanismus links unten zu einem Punkt zusammen. Wir erhalten die Situation des Umfangwinkelsatzes. Der Ergänzungsbogen kann weggelassen werden.

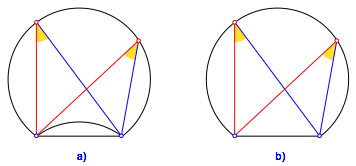
Abb. 3: Sonderfall Umfangwinkelsatz

4 Andere Dispositionen

Die Winkelinvarianz gilt auch, wenn wir die beiden Punkte symmetrisch außerhalb der Sehne setzen (Abb. 4a). Wir müssen dazu die Kreisbögen zu Kreisen ergänzen.

Wir können die beiden Kreise auch trennen (Abb. 4b).

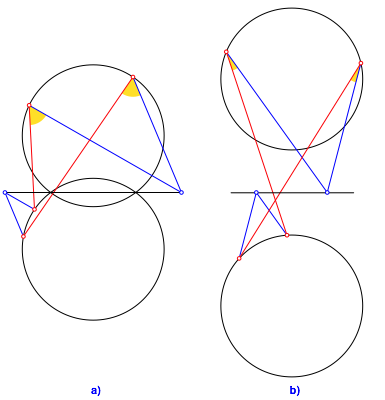
Abb. 4: Andere Dispositionen

5 Noch ein Sonderfall

Wenn wir die beiden Kreise aufeinandersetzen, ergeben sich — wer hätte das gedacht — rechte Winkel (Abb. 5a). Also eine Verallgemeinerung der Situation des Thaleskreises.

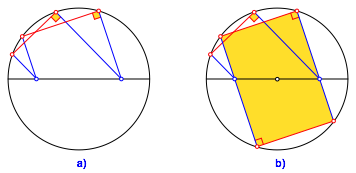
Abb. 5: Rechte Winkel

In diesem Sonderfall ist der Beweis recht einfach. Wir können die Konfiguration mit einer Punktspiegelung zu einem Rechteck ergänzen (Abb. 5b).

6 Beweis

Für den allgemeinen Fall ist mir kein schöner geometrischer Beweis gelungen. Nachfolgend ein rechnerischer Beweis mit kartesischen Koordinaten (Abb. 6).

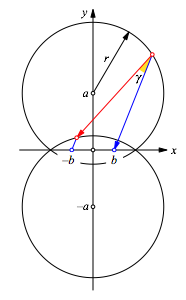
Abb. 6: Kartesisches Koordinatensystem

Die beiden Kreise haben die Koordinatengleichungen:

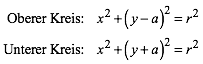(1)

Für die parallelen Geraden verwenden wir die Koordinatengleichungen:

(2)

Die etwas unübliche Verwendung des Steigungsparameters m erleichtert die Handhabung der senkrechten Geraden.

Der Rest ist Rechnung. Das höchste der Gefühle sind dabei quadratische Gleichungen. Für den Zwischenwinkel der beiden eingezeichneten Vektoren erhalten wir:

(3)

Die Parameter m und r kommen in (3) nicht vor. Der Winkel ist daher invariant gegenüber Änderungen von m, also Verdrehungen der beiden Parallelen. Dies war zu zeigen.

7 Beifang

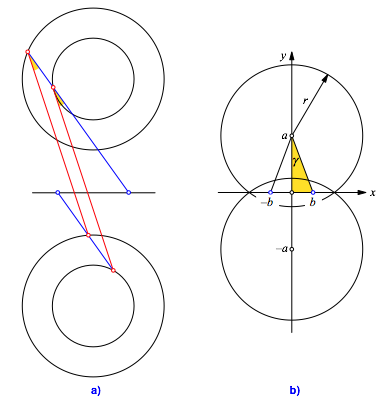
Abb. 7: Beifang

Der Kreisradius r kommt in (3) ebenfalls nicht vor. Der Winkel ist also auch invariant gegenüber Veränderungen des Kreisradius r (Abb. 7a).

Ebenfalls aus (3) sehen wir, dass der Winkel im gelb eingezeichneten Dreieck (Abb. 7b) erscheint. Im Sonderfall des Umfangwinkelsatzes ist das der halbe Zentriwinkel.

Weblink

Hans Walser: Ellipsentangente und Herzkurve

http://www.walser-h-m.ch/hans/Miniaturen/E/Ellipsentangente/Ellipsentangente.htm