1 Die Anregung

Ostern ist zwar vorbei, doch ist ein kombinatorisches Problem noch immer ungelöst: Der Osterhase macht Nester mit 5 Eiern. Es stehen rote, blaue und gelbe zur Wahl.

Dann gibt es bekanntlich 3•4•5•6•7/1•2•3•4•5 verschiedene Nester. Das kann man wie folgt interpretieren: Das erste ins Nest gelegte Ei hat 3 Möglichkeiten, was ja offensichtlich ist.

Aber wie kann man sich klar machen, dass das zweite Ei 4 Möglichkeiten, das dritte Ei 5 usw. haben soll?

2 Die schulische Lösung

Wir haben 5 Eier und zwei Farb-Trennstriche. Somit müssen wir aus 7 Positionen deren zwei für die Farb-Trennstriche auswählen. Gibt Lösungen. Die Abbildung 1 zeigt ein Beispiel.

Abb. 1: Beispiel

3 Partitionen

Gesucht sind alle Tripel (rot, blau, gelb) mit nichtnegativen ganzen Zahlen so dass .

Systematische Auflistung:

0, 0, 5	0, 1, 4	0, 2, 3	0, 3, 2	0, 4, 1	0, 5, 0
	1, 0, 4	1, 1, 3	1, 2, 2	1, 3, 1	1, 4, 0
		2, 0, 3	2, 1, 2	2, 2, 1	2, 3, 0
			3, 0, 2	3, 1, 1	3, 2, 0
				4, 0, 1	4, 1, 0
					5, 0, 0

Tab. 1: Systematische Auflistung

Es gibt 6 + 5 + 4 + 3 + 2 + 1 = 21 Lösungen.

Wir können die Zahlentripel als kartesische Koordinaten im Raum interpretieren und erhalten so 21 Punkte gemäß Abbildung 2.

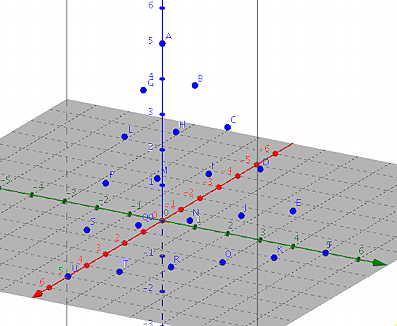
Abb. 2: Punkte im Raum

4 So geht es auch

Zunächst ist . Wir versuchen, die letzte Angabe zu interpretieren.

Wir arbeiten wieder mit Farbtrennstrichen rot/blau und blau/gelb.

Zu Beginn sieht die Sache für den Osterhasen so aus:

. / . / .

An jedem der drei Punkte kann er das erste Ei setzen, also 3 Möglichkeiten:

. 1 . / . / . und . / . 1 . / . und . / . / . 1 .

In jedem der drei Fälle hat der Osterhase nun für das zweite Ei vier Punkte zur Verfügung wo er das Ei setzen kann.

Aus der ersten Möglichkeit oben ergeben sich zum Breidpiel die vier Fälle:

. 2 . 1. / . / . und . 1 . 2 . / . / . und . 1 . / . 2 . / . und . 1 . / . / . 2 .

Für das dritte Ei gibt es jeweils 5 Möglichkeiten. Usw.

Wir haben also lineare Anordnungen. Da im Nest die Reihenfolge keine Rolle spielt, muss noch durch 5! dividiert werden.