Hans Walser, [20140107]

Parabel vierten Grades

Anregung, Idee und Hinweise: B. v. P., O.

1 Worum geht es?

Die Parabel vierten Grades mit zwei reellen Wendepunkten hat Schrägspiegelsymmetrie sowie einige Verhältniseigenschaften. Insbesondere kommen der Goldene Schnitt und das DIN-Format vor. Die beiden Wendepunkte spielen eine wichtige Rolle.

2 Beispiel

Die folgenden Abbildungen basieren auf der Parabel mit der Gleichung:

Die festgestellten Eigenschaften gelten aber für alle Parabeln vierten Grades mit zwei reellen Wendepunkten.

Beweise im nächsten Abschnitt.

2.1 Parabel

Die Parabel der Abbildung 1 hat auf den ersten Blick keine Symmetrie.

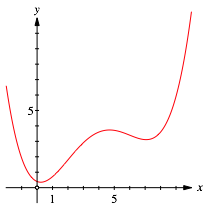
Abb. 1: Parabel vierten Grades

2.2 Wendepunkte

In der Abbildung 2 sind die beiden Wendepunkte eingetragen. Die Gerade durch die beiden Wendepunkte nennen wir Wendepunktgerade. Durch den Mittelpunkt der beiden Wendepunkte zeichnen wir eine zur y-Achse parallele Gerade.

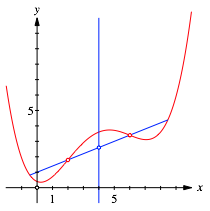
Abb. 2: Wendepunkte

Die Abbildung 2 lässt vermuten, dass die Parabel eine Schrägspiegelsymmetrie hat. Die Achse ist die zur y-Achse parallele Gerade, die Spiegelrichtung ist durch die Wendepunktgerade gegeben.

2.3 Spezielle Tangenten

In der Abbildung 3 ist zusätzlich unten die Tangente eingetragen, welche die Parabel zwei Mal berührt. Diese Tangente überbrückt die konkave Einbuchtung der Parabel. Die Tangente ist parallel zur Wendepunktgerade.

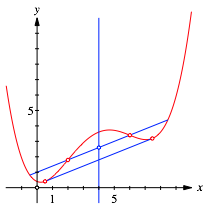
Abb. 3: Untere Tangente

Man beachte, dass die beiden Berührungspunkte der unteren Tangente nicht die lokalen Tiefpunkte der Parabel sind.

In der Abbildung 4 ist weiter die innere Tangente eingezeichnet, welche durch den Schnittpunkt der Achse mit der Parabel verläuft. Diese innere Tangente ist ebenfalls parallel zur Wendepunktgerade.

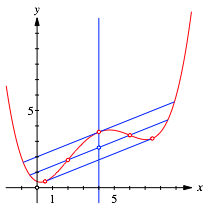
Abb. 4: Innere Tangente

Der Berührungspunkt der inneren Tangente ist nicht der lokale Hochpunkt der Parabel.

2.4 Teilverhältnisse

2.4.1 Wendepunktgerade

Die Wendepunktgerade teilt den durch die untere und die innere Tangente gegebenen Streifen (Abb. 4) im Breitenverhältnis 4 : 5. Dies gilt nicht nur für unser Beispiel, sondern für alle Parabeln vierten Grades mit zwei reellen Wendepunkten.

2.4.2 Goldener Schnitt

Die vier in der Abbildung 5 eingezeichneten Punkte auf der Wendepunktgeraden, also die beiden Wendepunkte und die beiden äußeren Schnittpunkte der Wendepunktgeraden mit der Parabel, teilen im Verhältnis des Goldenen Schnittes, und zwar in der Reihenfolge Minor-Major-Minor (der Dicke in der Mitte). Über den Goldenen Schnitt vergleiche (Walser, 2013a).

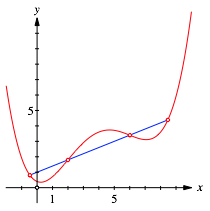
Abb. 5: Goldener Schnitt

Wir können das mit Goldenen Rechtecken illustrieren (Abb. 6).

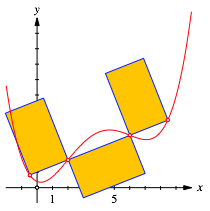
Abb. 6: Goldene Rechtecke

2.4.3 DIN-Format

Der Abschnitt der inneren Tangente zwischen den beiden äußeren Schnittpunkten mit der Parabel ist mal so lang wie der Abschnitt der unteren Tangente zwischen den beiden Berührungspunkten. Hier kommt das Seitenverhältnis des DIN-Formates ins Spiel. Über das DIN-Format vergleiche (Walser, 2013b). Die Abbildung 7 illustriert das mit einem Rechteck im DIN-Format.

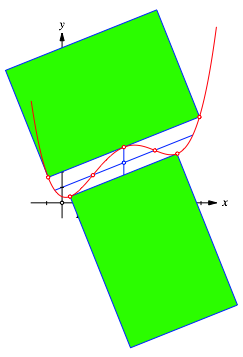
Abb. 7: Rechtecke im DIN-Format

Natürlich lässt sich das auch mit rechtwinklig gleichschenkligen Dreiecken illustrieren (Abb. 8).

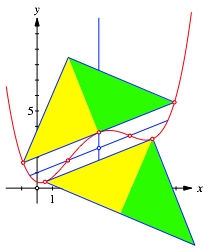
Abb. 8: Rechtwinklig gleichschenklige Dreiecke

2.5 Flächenverhältnisse

2.5.1 Flächengleichheit

Die beiden roten Flächen (Abb. 9) sind gleich groß und zusammen so groß wie die zyanfarbene Fläche. Diese wird durch die Achse halbiert.

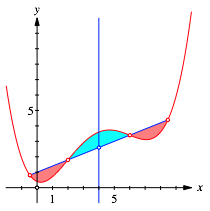
Abb. 9: Gleiche Flächen

2.5.2 Nochmals die Quadratwurzel aus 2

Die beiden grünen Flächen (Abb. 10) sind gleich groß und zusammen mal so groß wie die gelbe Fläche.

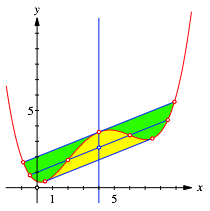
Abb. 10: Flächenfaktor Wurzel aus 2

3 Beweis

3.1 Affine Invarianz

Die in unseren Feststellungen verwendeten Begriffe Wendepunkt, Parallelität, Teilverhältnis und Flächenverhältnis sind affin invariant. Bei einer affinen Abbildung, welche die Richtung der y-Achse invariant lässt, ist auch der Begriff Parabel vierten Grades invariant.

3.2 Affine Standardisierung

Wir standardisieren die Parabel vierten Grades mit einer affinen Abbildung so, dass die beiden Wendepunkte auf die Punkte mit den Koordinaten und zu liegen kommen. Ferner soll die Parabel durch den Punkt verlaufen. Wir beschreiben die Parabel also in dem in der Abbildung 11 angedeuteten blauen Koordinatensystem.

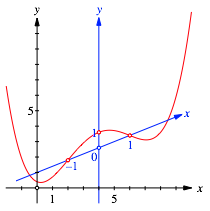
Abb. 11: Affin verzerrtes Koordinatensystem

Aus dem Ansatz

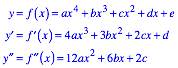
erhalten wir:

Dieses Gleichungssystem hat die Lösung:

In diesem blauen Koordinatensystem erhält die Parabel also die standardisierte Gleichung:

Dies ist eine gerade Funktion, womit die Symmetrie durch die Schrägspieglung nachgewiesen ist.

Die Funktionsformel lässt sich faktorisieren:

Freude herrscht, weil erscheint.

3.2.1 Teilverhältnisse

In orthonormierten kartesischen Koordinatensystem sieht diese Parabel gemäß Abbildung 12 aus. Es sind auch die Koordinaten der relevanten Punkte eingetragen, ein Eldorado in Quadratwurzeln. Aus diesen Koordinaten lassen sich alle oben festgestellten Teilverhältnisse ablesen.

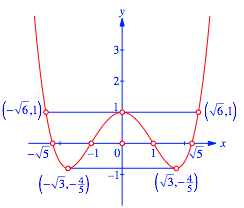
Abb. 12: Standardisierte Parabel

3.2.2 Flächenverhältnisse

Die Abbildung 13 illustriert das erste Flächenverhältnis.

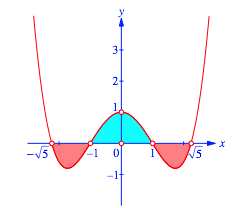
Abb. 13: Erstes Flächenverhältnis

Für die rote Fläche erhalten wir:

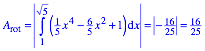
Für die zyanfarbene Fläche ergibt sich:

Damit haben wir die Flächenverhältnisse in der Reihenfolge 1 : 2 : 1.

Die Abbildung 14 illustriert das zweite Flächenverhältnis.

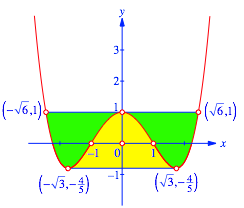
Abb. 14: Zweites Flächenverhältnis

Für die grüne Fläche ergibt sich:

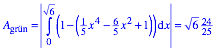
Für die gelbe Fläche ergibt sich:

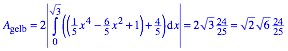
Somit haben wir die Flächenverhältnisse in der Reihenfolge .

Literatur

Walser, Hans (2013a). Der Goldene Schnitt. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. 6. Auflage. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.