1 Worum geht es?

Vier kozyklische Punkte.

2 Konstruktion

Wir beginnen mit einer durch Brennpunkt und Leitlinie gegebenen Parabel (Abb. 1). In einem beliebigen Parabelpunkt zeichnen wir die Tangente.

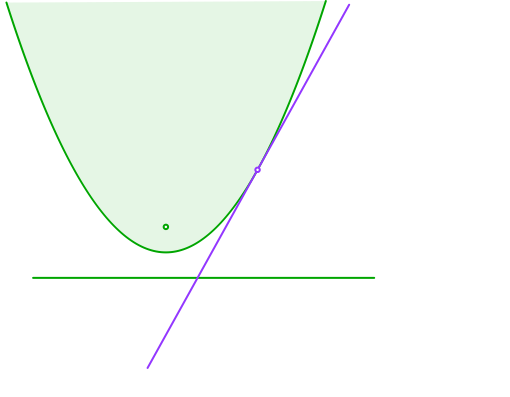
Abb. 1: Parabel und Tangente

Nun spiegeln wir die Parabel mitsamt Brennpunkt und Leitlinie an der Tangente (Abb. 2). Der Brennpunkt der einen Parabel liegt auf der Leitlinie der anderen und umgekehrt. Beweis folgt.

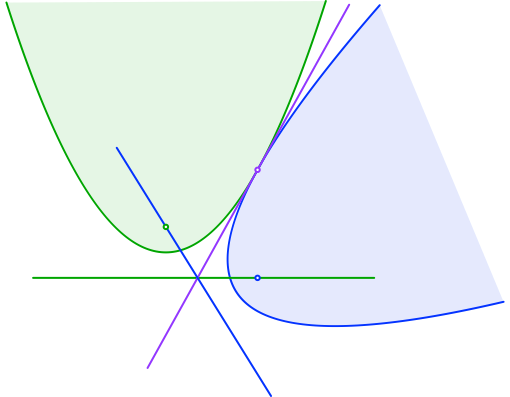
Abb. 2: Gespiegelte Parabel

Die beiden Brennpunkte, der Berührungspunkt der beiden Parabeln und der Schnittpunkt der beiden Leitlinien liegen auf einem Kreis (Abb. 3).

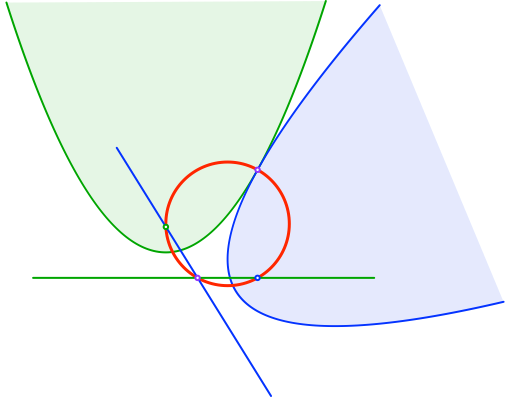
Abb. 3: Vier kozyklische Punkte

Die Abbildung 4 zeigt eine Animation dazu. Die blaue Parabel wird auf der grünen Parabel abgerollt.

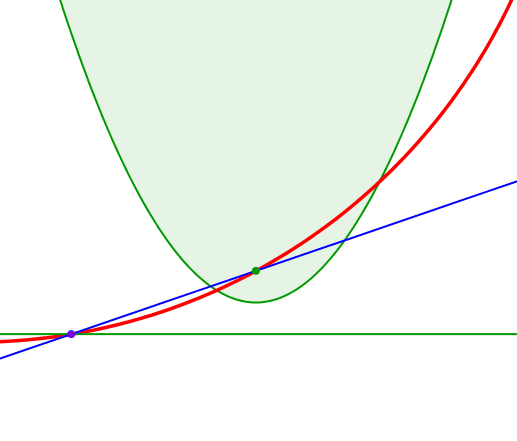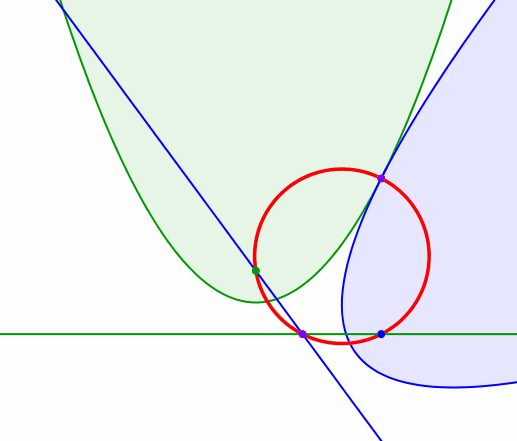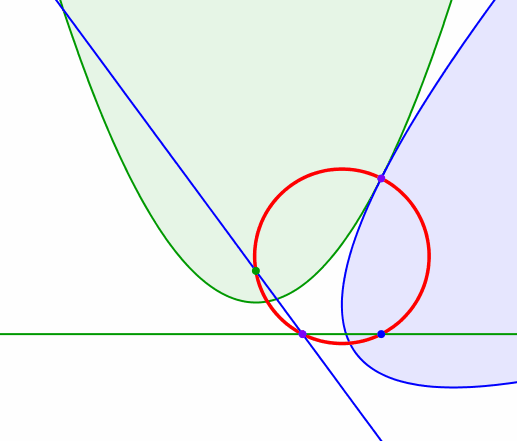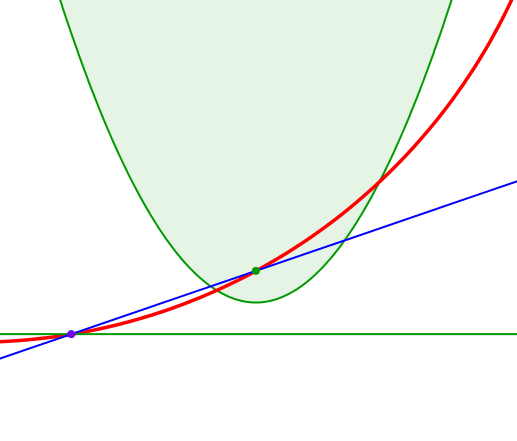
Abb. 4: Animation

3 Beweis

Auf Grund der Abstandsdefinition der Parabel sind die beiden in der Abbildung 5 eingezeichneten schwarzen Strecken gleich lang. Wegen der Reflexionseigenschaft der Parabel ist die Tangente die Winkelhalbierende der beiden Strecken.

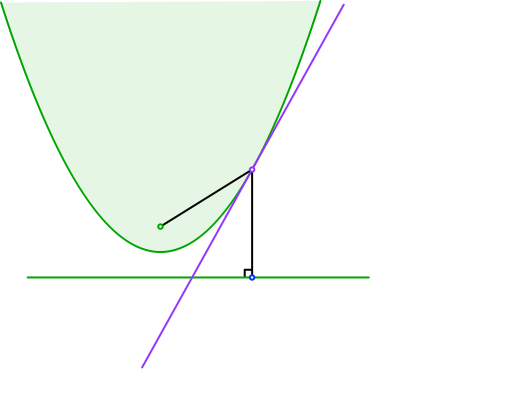
Abb. 5: Abstandsdefinition und Reflexionseigenschaft

Nach dem Spiegeln haben wir daher die Situation der Abbildung 6. Der Brennpunkt der einen Parabel liegt auf der Leitlinie der anderen Parabel und umgekehrt. Das gelb markierte Viereck ist ein Drachenviereck mit zwei gegenüberliegenden rechten Winkeln und daher ein Sehnenviereck. Dies war zu zeigen.

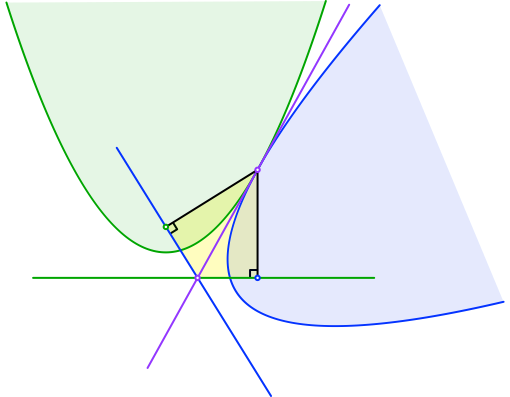
Abb. 6: Situation nach dem Spiegeln

Weblinks

Hans Walser: Kegelschnitte abrollen

http://www.walser-h-m.ch/hans/Miniaturen/K/Kegelschnitte_abrollen/Kegelschnitte_abrollen.html