Hans Walser, [20111203a]

Parabelhalbierung

Anregung: J. H., A.

1 Problemstellung

Das blaue Flächenstück zwischen dem Parabelbogen und der x-Achse soll halbiert werden.

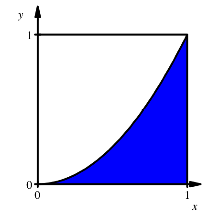
Das blaue Flächenstück soll halbiert werden

Das blaue Flächenstück hat den Flächeninhalt:

2 Halbierungsschnitte

2.1 Vertikaler Schnitt

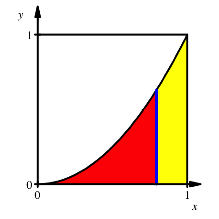
Vertikaler Schnitt

Für die Schnittgerade erhalten wir die Bedingung:

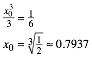
Das Problem entspricht dem klassischen Würfelverdoppelungsproblem.

2.2 Horizontaler Schnitt

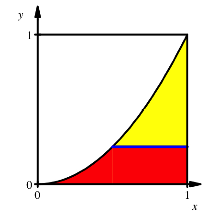
Horizontaler Schnitt

Den Schnittpunkt der horizontalen Schnittgeraden mit der Parabel habe die Koordinaten . Wir erhalten die Flächenbedingung:

Daraus ergibt sich die kubische Gleichung:

Diese hat die drei Lösungen . Die in unserem Problem relevante Lösung ist .

2.3 Schnitt mit Ursprungsgerade

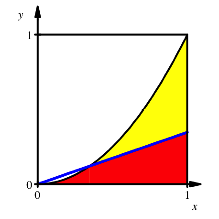
Schnitt mit Ursprungsgerade

Den Schnittpunkt der Ursprungsgeraden mit der Parabel habe die Koordinaten . Die Ursprungsgerade hat daher die Steigung und die Gleichung . Das untere Flächenstück setzt sich aus einem Stück Fläche unter der Parabel (bis ) und einem Trapez zusammen. Wir erhalten die Flächenbedingung:

Daraus ergibt sich die kubische Gleichung:

Diese hat die drei Lösungen . Es sind keine „schöne“ Lösungen. Die in unserem Problem relevante Lösung ist .

2.4 Schnitt mit Ecktransversale unten rechts

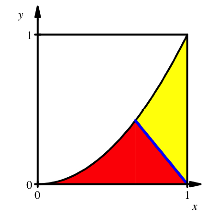
Schnitt mit Ecktransversale unten rechts

Den Schnittpunkt der Ecktransversalen mit der Parabel habe die Koordinaten . Wir erhalten damit die Flächenbedingung:

Daraus ergibt sich die kubische Gleichung:

Diese hat die drei Lösungen . Es sind keine „schöne“ Lösungen. Die in unserem Problem relevante Lösung ist .

2.5 Schnitt mit Ecktransversale oben rechts

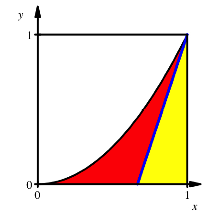
Schnitt mit Ecktransversale oben rechts

Die Sache ist einfach. Die Ecktransversale hat die Gleichung .

2.6 Schnitt mit Ecktransversale oben links

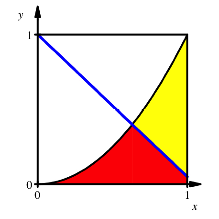
Schnitt mit Ecktransversale oben links

Den Schnittpunkt der Ecktransversalen mit der Parabel habe die Koordinaten . Die Ecktransversale hat dann die Gleichung:

Wir erhalten die Flächenbedingung:

Daraus ergibt sich die Gleichung vierten Grades:

Diese hat die Lösungen . Die in unserem Problem relevante Lösung ist .

3 Diagonalenschnitt

Die Beispiele 2.4 und 2.6 zeigen, dass die Diagonale von links oben nach rechts unten die Fläche nicht halbiert. Hingegen erhalten wir den Goldenen Schnitt. Die Diagonale hat die Gleichung . Für den Schnittpunkt mit der Parabel ergibt sich .

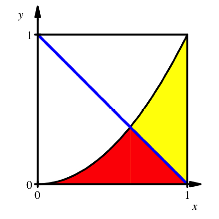
Diagonalenschnitt

Die rote Fläche ist , also kleiner als die Hälfte von , die gelbe Fläche .

4 Doppelschnitt

Wir zerschneiden vertikal wie in Beispiel 2.1, aber mit zwei parallelen Schnittgeraden im Abstand . Der Flächeninhalt zwischen den beiden vertikalen Schnittgeraden (in der Abbildung gelb) soll gleich der Summe der Flächeninhalte der beiden äußeren Teile (rot) sein. Die beiden Schnittlinien haben die Gleichungen beziehungsweise .

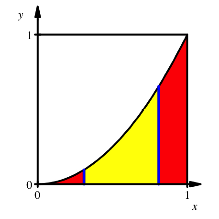
Doppelschnitt

Die Flächenbedingung liefert:

Bei dieser Gleichung fällt der kubische Anteil heraus und es bleibt eine quadratische Gleichung übrig:

Diese hat also positive Lösung:

Für die zweite Schnittgerade erhalten wir:

Die beiden Schnittgeraden haben also die Gleichungen beziehungsweise . Wir erhalten je die Hälfte des „kleinen“ und des „großen“ Goldenen Schnittes.

5 Variante der Parabel

Wir arbeiten mit der Parabel . Der blaue Flächeninhalt der Figur ist .

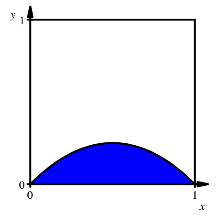
Variante

5.1 Schnitt mit Ursprungsgerade

Wir schneiden mit einer Geraden .

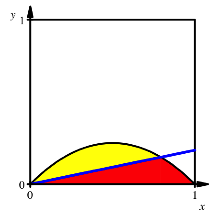
Schnitt mit Ursprungsgeraden

Für den Schnittpunkt mit der Parabel erhalten wir die Bedingung:

Diese quadratische Gleichung hat die Lösungen . Wir führen daher die Notation ein. Die Schnittgerade hat nun also die Steigung . Geometrisch ist p also der Abschnitt am rechten Quadratrand von der Ecke rechts oben bis hinunter zur Schnittgeraden.

Der Schnittpunkt der Schnittgeraden mit der Parabel hat die Koordinaten . Für den roten Flächenanteil ergibt sich:

Wenn die Schnittlinie nun die Parabelfläche halbieren soll, haben wir die Bedingung:

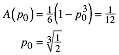
Das ist wiederum eine Variante des klassischen Würfelverdoppelungsproblem.

5.2 Doppelschnitt mit Ursprungsgeraden

Wir schneiden mit zwei Ursprungsgeraden, deren Steigungen sich um unterscheiden sollen. Dann unterscheiden sich auch die p-Werte um . Und es soll die Fläche zwischen den beiden Ursprungsgeraden die halbe Parabelfläche ausmachen.

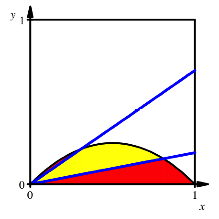
Doppelschnitt

Die Flächenbedingung liefert:

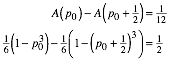
In dieser kubischen Gleichung fällt der kubische Anteil weg und es bleibt eine quadratische Gleichung übrig:

Diese hat die positive Lösung:

Die obere Schnittgerade hat also die Steigung , die untere Schnittgerade die Steigung .