Hans Walser, [20111205b]
Parabelkonstruktion
1
Konstruktion
Auf der
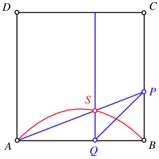
Seite BC eines Quadrates ABCD wŠhlen wir einen variablen Punkt P. Dann
verfahren wir gemŠ§ Figurenfolge. Der Punkt S
beschreibt eine Parabel.
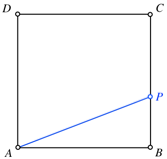
Strecke AP
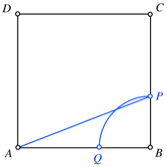
Kreisbogen
um B
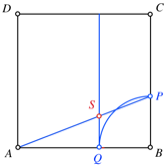
Senkrechte
in Q. Schnittpunkt S
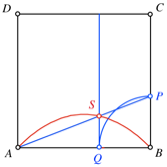
Parabelbogen
2
Beweis
Wir
verwenden ein kartesisches Koordinatensystem mit dem Ursprung in A und Einheitspunkten in B beziehungsweise D. Weiter sei m die y-Koordinate des Punktes P. Die Strecke AP hat die Gleichung 
und die
Senkrechte in Q die Gleichung 
. Fźr den Schnittpunkt S ergibt
sich:
Elimination
des Parameters m liefert fźr S die Parabelgleichung 
.
3
Variante
Wir
ersetzen den Viertelbogen durch eine Parallele zur Diagonalen AC.
Variante