Hans Walser, [20080113a]
Parabeln
Anregung: Archimedes. [Netz/Noel 2007]
1 Worum es geht
Es werden Parabeln mit Hilfe von VerhŠltnissen punktweise konstruiert.
2 Grundkonstruktion
Wir wŠhlen einen Punkt 
auf der
Basislinie des Einheitsquadrates und konstruieren dann den Punkt P gemŠ§ der in der Figur angedeuteten Reihenfolge.
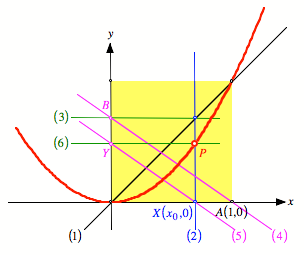
Konstruktion
Der Punkt P liegt auf der Parabel 
.
Zur BegrŸndung die
Bezeichnungen 
und 
. Wegen (1), (2) und (3) ist 
. Da (4) und (5) parallele Geraden sind, folgt:
Wegen 
erhalten wir
daraus:
Wir haben eine so
genannte ãmittlere ProportionaleÒ 
. Es ist: 
.
Mit Cabri-GŽomtre
lŠsst sich dann mit dem Befehl Ortskurve
die Parabel zeichnen. Es empfiehlt sich dabei, fŸr 
nur ein
beschrŠnktes Intervall auf der Basislinie zuzulassen, eine Strecke also, statt
der ganzen Geraden. Cabri-GŽomtre hat sonst Schwierigkeiten.
Die Konstruktion
funktioniert auch fŸr negative 
.
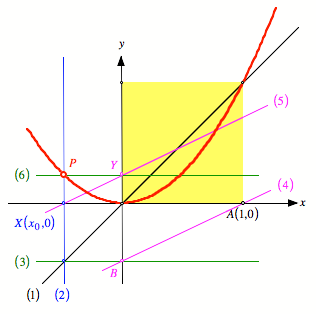
Negativer x0-Wert
3
Affine Verallgemeinerung
Wir kšnnen das
Einheitsquadrat durch ein Parallelogramm ersetzen.
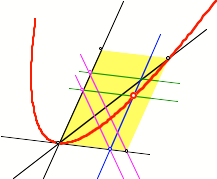
Affine Verzerrung
4
Parabeln hšheren Grades
Wenn wir das VerhŠltnis
ein weiteres Mal
Ÿbertragen, ergibt sich eine kubische Parabel.
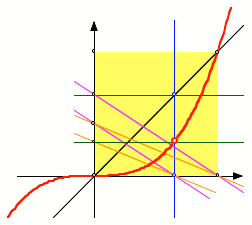
Kubische Parabel
Und so weiter.
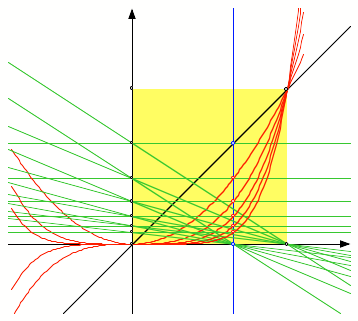
Parabeln der Grade 2 bis
6
5
Negative Exponenten
Durch eine kleine
Modifikation erhalten wir 
. Das VerhŠltnis wird umgekehrt abgetragen.
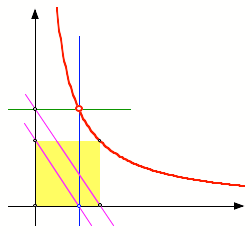
Grad –1
Auch das lŠsst sich
weiterfŸhren.
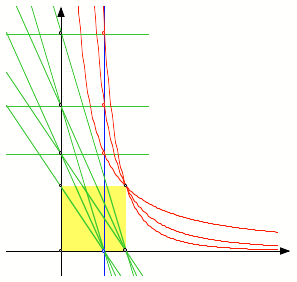
Grade –1,
–2, –3
Literatur
[Netz/Noel 2007] Netz, Reviel und Noel,William: Der Kodex des Archimedes. Das berŸhmteste Palimpsest der Welt wird entschlŸsselt. Aus dem Englischen von Thomas Filk. 2. Auflage. MŸnchen: Verlag C. H. Beck 2007. ISBN 978 3 406 56336 2