1 Worum geht es?

Figuren. Sonst nichts.

2 Allgemeines Dreieck

Die Abbildung 1 zeigt ein „allgemeines“ (unregelmäßiges) Dreieck in der klassischen zyklischen RGB-Färbung.

Abb. 1: Unregelmäßiges Dreieck

Nun zeichnen wir die Parabel mit der roten Seite als Leitlinie und der roten Ecke als Brennpunkt ein (Abb. 2).

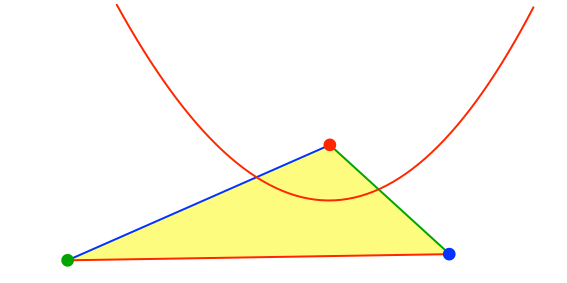
Abb. 2: Rote Parabel

Die Parabel berührt die rote Mittelparallele des Dreiecks (Abb. 3).

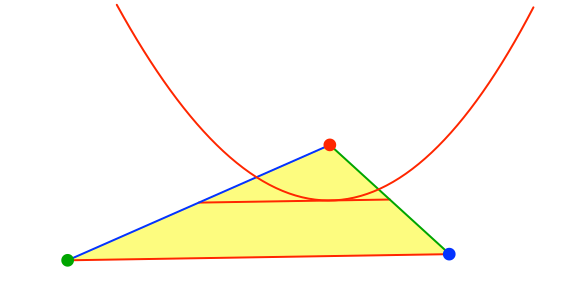
Abb. 3: Mittelparallele

Analog zeichnen wir die grüne und die blaue Parabel (Abb. 4).

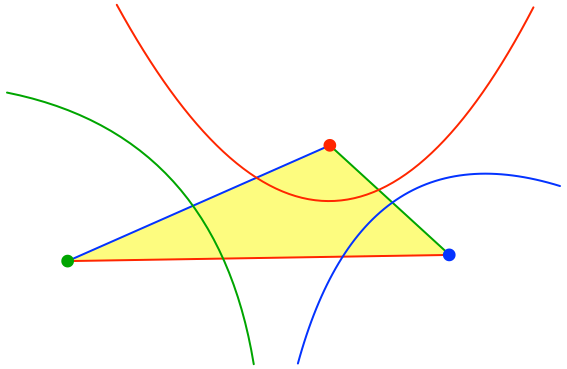
Abb. 4: Alle drei Parabeln

Die drei Parabeln sind disjunkt. Sie haben keine gemeinsamen Punkte. Ist dies allgemein so?

Nehmen wir einmal an, die blaue und die grüne Parabel hätten einen gemeinsamen Punkt (Abb. 5).

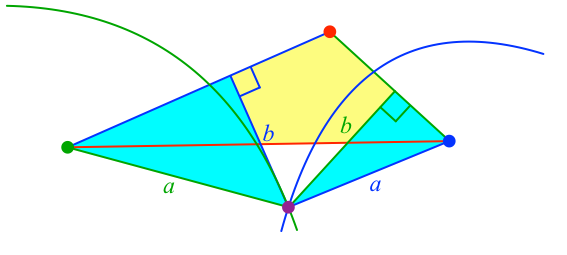
Abb. 5: Gemeinsamer Punkt

Aufgrund der Abstandsdefinition der grünen Parabel ist dann:

a = b

Analog gilt für die blaue Parabel:

a = b

Wegen der hellblau eingezeichneten rechtwinkligen Dreieck gelten die beiden Ungleichungen:

a ≥ b und a ≥ b

Wir haben also die Ungleichungskette:

a ≥ b = a ≥ b = a

Damit haben wir eine sogenannte „exakte Abschätzung“. Es müssen alle vier Strecken gleich groß sein:

a = b = a = b

Dies ist nur im gleichschenkligen Dreieck möglich (Abb. 6).

Im gleichschenkligen Dreieck berühren sich die beiden symmetrisch liegenden Parabeln auf der Symmetrieachse (Abb. 6).

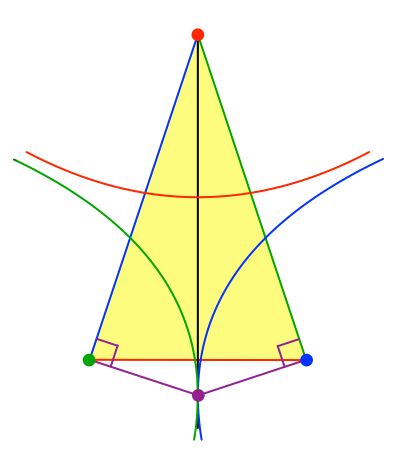
Abb. 6: Gleichschenkliges Dreieck

Das gleichseitige Dreieck ist in dreifacher Hinsicht gleichschenklig. Daher berühren sich die drei Parabeln paarweise (Abb. 7).

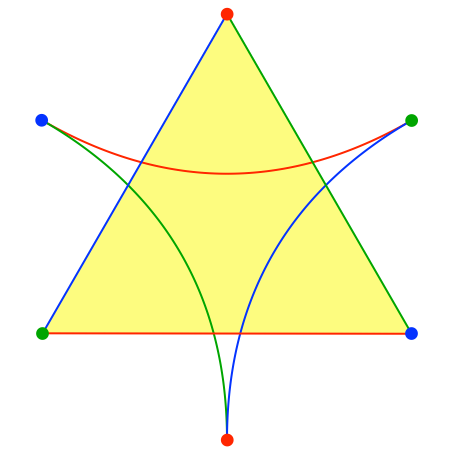
Abb. 7: Gleichseitiges Dreieck

Die Berührungspunkte liegen auf dem Umkreis des Dreieckes und ergänzen die Dreiecksecken zum regelmäßigen Sechseck (Abb. 8).

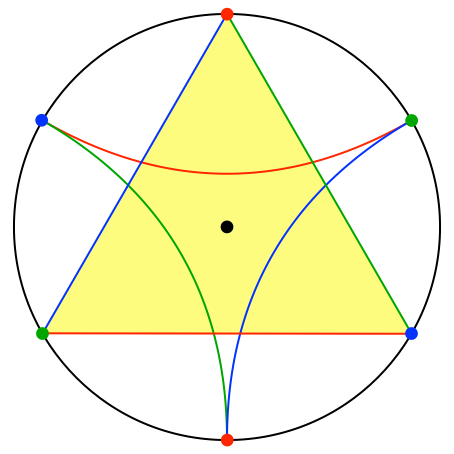
Abb. 8: Umkreis

Die Parabeln berühren das Kantenmittendreieck und dessen Inkreis (Abb. 9).

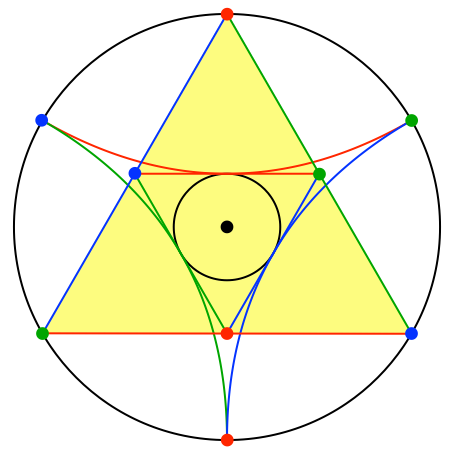
Abb. 9: Kantenmittendreieck

Die Figur kann zu einem Stern mit sechs Spitzen ergänzt werden (Abb. 10).

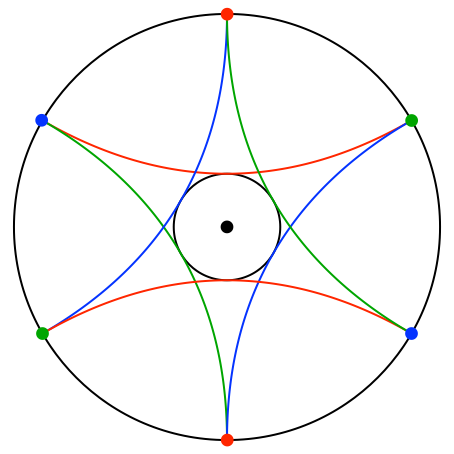
Abb. 10: Stern

Die Abbildung 11 zeigt den Vergleich mit dem Dreispitz von Steiner.

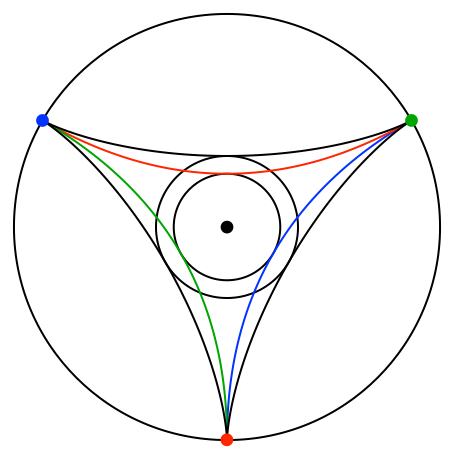
Abb. 11: Dreispitz