Hans Walser, [20180706]

Parabelnormalen

1 Worum geht es?

Von einem beliebigen Punkt A aus sollen die Normalen an eine gegebene Parabel p gelegt werden. Wie viele Lösungen gibt es?

2 Beispiele

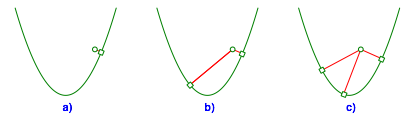
Abb. 1: Ausgangspunkt im Innern der Parabel

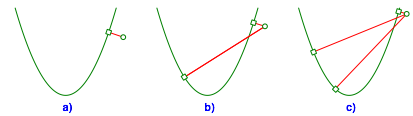
Abb. 2: Ausgangspunkt außerhalb der Parabel

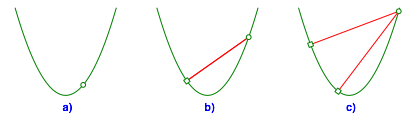
Abb. 3: Ausgangspunkt auf der Parabel

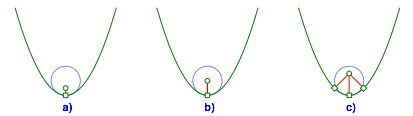
Abb.4: Ausgangspunkt auf der Symmetrieachse

Die Frage ist natürlich, in welchen Fällen für die Lage des Ausgangspunktes A es wie viele Lösungen gibt.

3 Berechnung

Dem Ausgangspunkt A geben wir die Koordinaten . Weiter sei ein laufender Punkt auf der Standardparabel p.

Für eine von A ausgehende Normale (Lot) auf p muss die Distanz oder (rechnerisch einfacher) das Quadrat davon extremal sein. Wir haben also die Bedingung:

(1)

Daraus ergibt sich:

(2)

Oder umgeformt:

(3)

Wir haben die kubische Gleichung (3) nach x aufzulösen.

3.1 Beispiele

Die Abbildungen 5 bis 8 zeigen die grafische Auflösung der Gleichung (3) entsprechend den Beispielen der Abbildungen 1 bis 4.

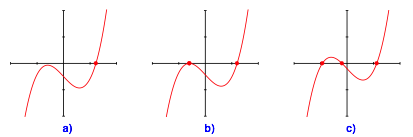
Abb. 5: Ausgangspunkt im Innern der Parabel

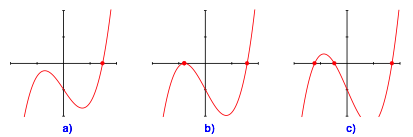
Abb. 6: Ausgangspunkt außerhalb der Parabel

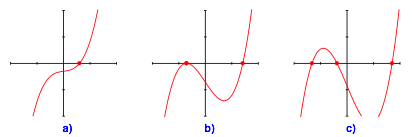
Abb. 7: Ausgangspunkt auf der Parabel

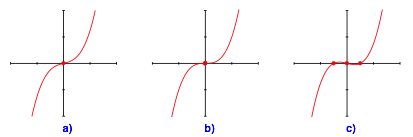
Abb. 8: Ausgangspunkt auf der Symmetrieachse

3.2 Allgemein

Zur Darstellung der Lösungen der allgemeinen Gleichung (3) verwenden wir die sogenannte Diskriminante D:

(4)

Weiter führen wir folgende Abkürzungen ein

(5)

sowie:

(6)

Damit können wir die Lösungen von (3) schreiben:

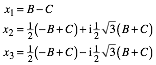(7)

4 Diskriminante und Evolute

Die Diskriminante D gibt Auskunft über das Lösungsverhalten:

· D > 0: Genau eine reelle Lösung (Abbildungen 1a bis 8a)

· D = 0: Interessanter Sonderfall (Abbildungen 1b bis 8b). In der Regel zwei Lösungen

· D < 0: Drei reelle Lösungen (Abbildungen 1c bis 8c)

Wo liegen die Punkte A mit D = 0? Also:

(8)

Die Abbildung 9 zeigt einen Implicitplot von (8), zusammen mit der Standardparabel p.

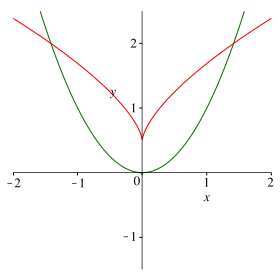
Abb. 9: Diskriminante null

Die rote Kurve ist die Evolute e der Parabel p. Die Evolute e der Standardparabel p hat die Parameterdarstellung:

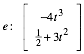(9)

Durch Einsetzen in (8) können wir nachweisen, dass wir es tatsächlich mit der Evolute zu tun haben.

Für Ausgangspunkte A oberhalb der Evolute e haben wir eine negative Diskriminante und damit drei Normalen auf die Parabel p.

Für Ausgangspunkte A unterhalb der Evolute e haben wir eine positive Diskriminante und damit genau eine Normale auf die Parabel p.

Die Abbildung 10 zeigt die Niveaulinien der Diskriminante für die Niveaus –200, –180, ... , 180, 200.

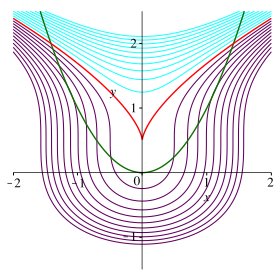
Abb. 10: Niveaulinien

Websites

Hans Walser: Parabel, Evolute und das DIN-Format (abgerufen 07.07.2018):

www.walser-h-m.ch/hans/Miniaturen/P/Parabelevolute_DIN/Parabelevolute_DIN.htm