Hans Walser, [20220318]
Parabelstern
1 Worum geht es
Spielerei mit Parabeln verschiedener Grade.
2 Einführungsbeispiel
Wir zeichnen exemplarisch mit quadratischen Parabeln einen Stern mit fünf Spitzen (Abb. 1). Im Folgenden sei a = 2 (Grad der Parabel) und e = 5 (Eckenzahl).

Abb. 1: Stern mit fünf Spitzen
Wir machen für die Parabel den Ansatz:
![]()
Wir passen nun einen Parabelbogen so ein, dass er die Ursprungsgerade berührt, welche mit der positiven y-Achse einen Winkel von 36° (allgemein: 180°/e, im Bogenmaß π/e) einschließt (Abb. 2). Den Parabelbogen zeichnen wir von der y-Achse bis zum Berührpunkt. Die Ursprungsgerade wird vom Ursprung bis zum Berührpunkt gezeichnet.
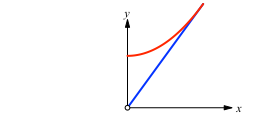
Abb. 2: Parabelbogen
Wir suchen also x0 (die Berührstelle) so, dass:
![]()
Daraus ergibt sich:
![]()
Nun spiegeln wir den gezeichneten Parabelbogen an der y-Achse (Abb. 3).
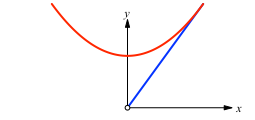
Abb. 3: Spiegeln
Zwischenbemerkung: Bei einer quadratischen Parabel hätten wir natürlich direkt die beiden Parabeläste zeichnen können. Anders ist die Sache bei einem gebrochenen Exponenten a, zum Beispiel bei a = 3/2 (Neilsche Parabel).
Durch Fünfteldrehungen erhalten wir schließlich den Parabelstern (Abb. 1).
3 Variation des Parabelgrades
In der Abbildung 4 variiert der Grad in halbzahligen Schritten von 3/2 bis 51.
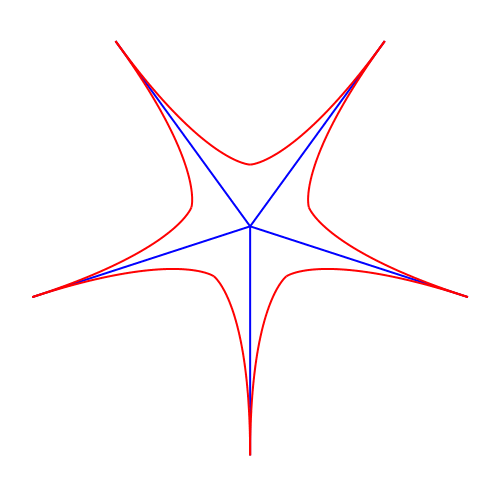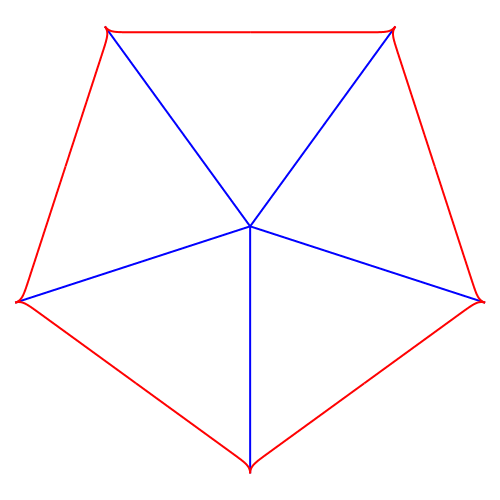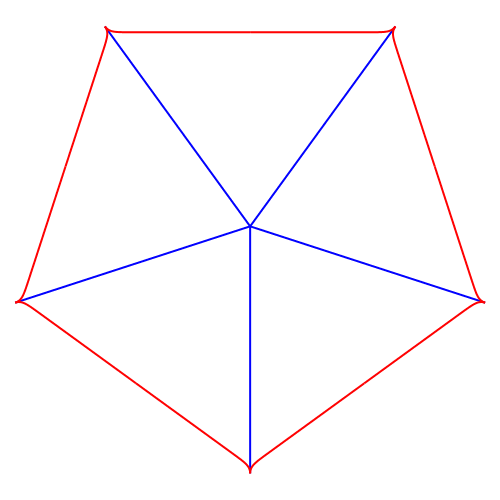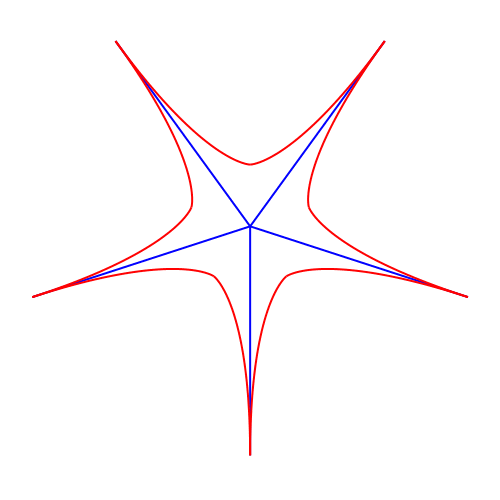
Abb. 4: Variation des Parabelgrades
4 Andere Eckenzahlen

Abb. 5: Mein Hut der hat drei Ecken
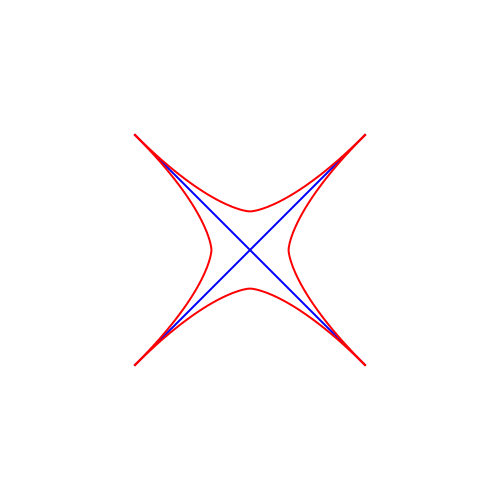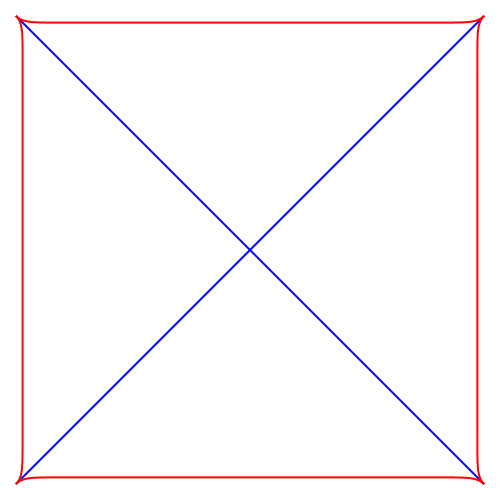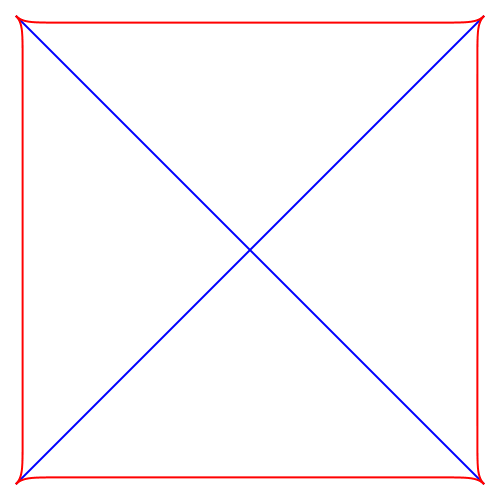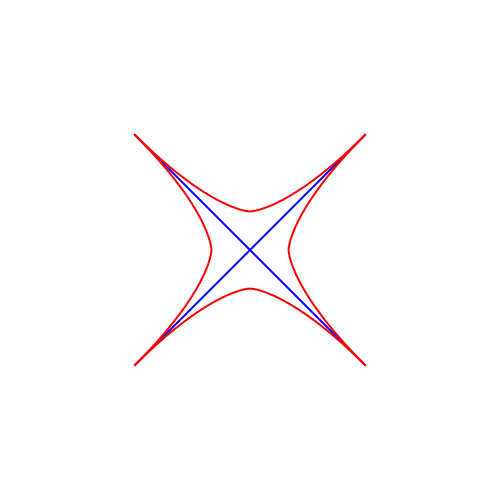
Abb. 6: Quadratisches

Abb. 7: Pentagramm
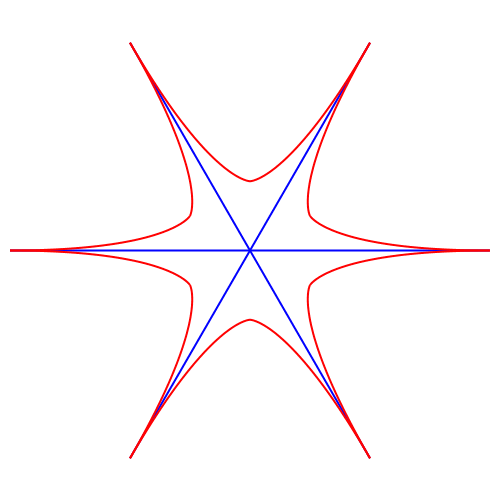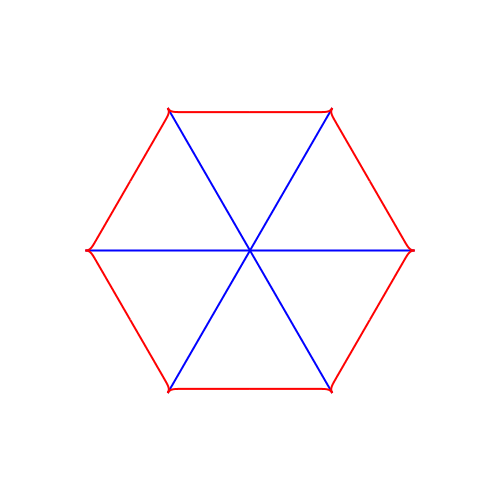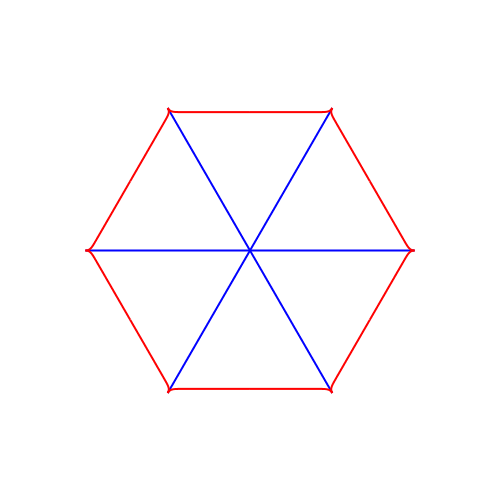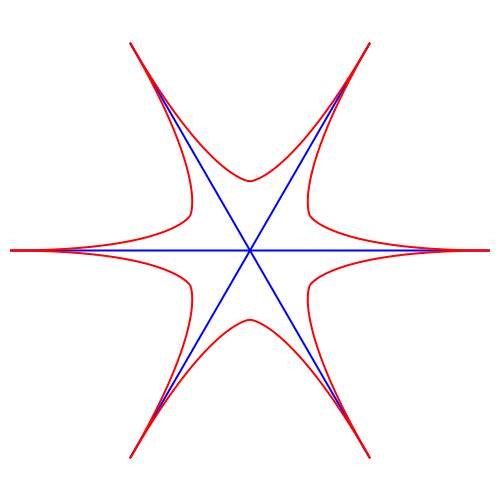
Abb. 8: Hexagon
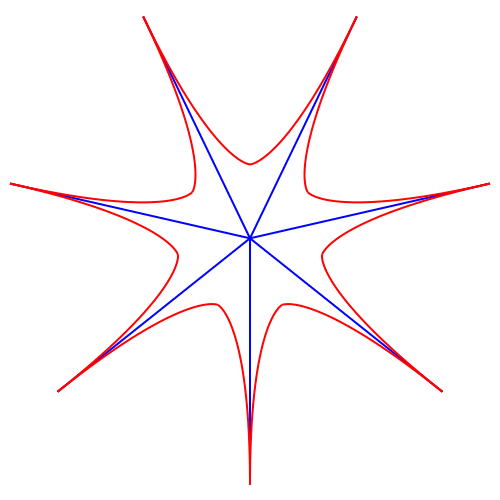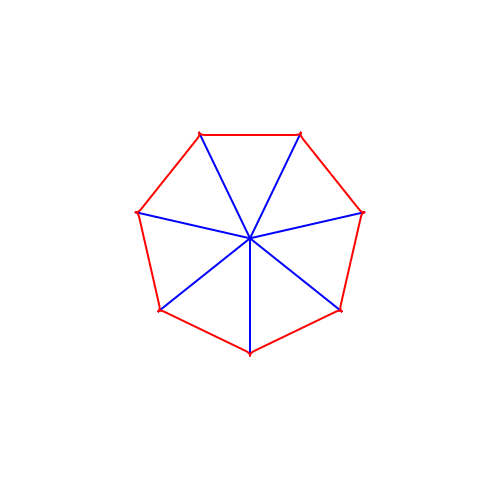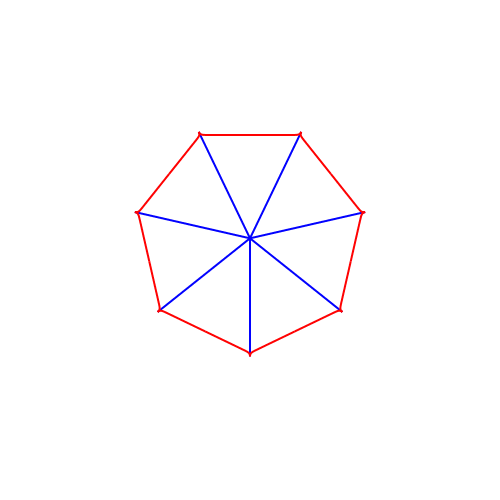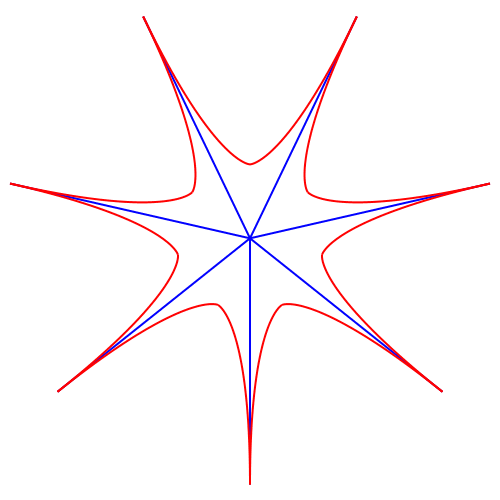
Abb. 9: Sieben zum Ersten

Abb. 10: Sieben zum Zweiten

Abb. 11: Sieben zum Dritten