Hans Walser, [20150413]

Parabelzirkel

Anregung: Chr. H., M. und H. H., W.

1 Was sind Parabelzirkel

Unter einem Parabelzirkel verstehe ich ein mechanisches Gerät, welches das Zeichnen einer Parabel erlaubt. Es gibt viele Beispiele dazu. Die Beispiele lassen sich in der Regel mit dynamischer Geometrie Software modellieren.

Im Folgenden werden einige mir bisher nicht bekannte Beispiele vorgestellt.

2 Einfaches Beispiel

In einem kartesischen Koordinatensystem zeichnen wir die Gerade a: x = 1 und zu einem beliebigen Parameterwert t die Gerade b: x = t (Abb. 1). Weiter zeichnen wir die Gerade c: y = t – x.

Abb. 1: Die beiden ersten Schritte

Nun zeichnen wir die Gerade d: y = t und die Gerade e: y = tx (Abb. 2).

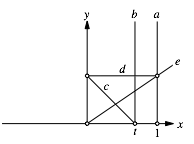
Abb. 2: Dritter und vierter Schritt

Der Schnittpunkt S von b mit e beschreibt die Parabel p (Abb. 3).

Abb. 3: Parabel

Rechnerisch ist die Sache einfach: Der Schnittpunkt S von b: x = t und e: y = tx hat die Koordinaten , liegt also auf der schulischen Standardparabel .

3 Etwas komplizierter

Wir beginnen mit einem Parallelogramm ABCD und einem Punkt E (Abb. 4).

Abb. 4: Startsituation

Nun wählen wir auf der Seite AB einen beliebigen Punkt P und zeichnen durch diesen Punkt P eine Parallele zur Seite BC. Diese Parallele schneiden wir mit der Diagonalen AC (Schnittpunkt F). Durch F zeichnen wir eine Parallele zur Seite AB und schneiden diese Parallele mit der Seite AD (Schnittpunkt G). Der Schnittpunkt S der Geraden PF und EG beschreibt die Parabel (Abb. 5). Die Symmetrieachse der Parabel ist parallel zur Seite BC.

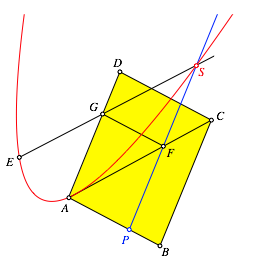
Abb. 5: Parabel

Das Verfahren ist im Prinzip eine Verallgemeinerung des einfachen Beispiels oben.

4 Noch allgemeiner

Dieses Verfahren ist sehr einfach zu beschreiben.

Wir beginnen mit einem beliebigen Viereck ABCD, welches kein Parallelogramm ist, und unterteilen die Seiten AB und DC im gleichen Verhältnis (Teilpunkte P und Q). Nun unterteilen wir noch die Strecke PQ in diesem Verhältnis (Teilpunkt S). Der Punkt S beschreibt die Parabel (Abb. 6).

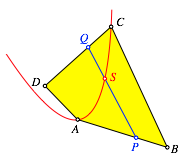
Abb. 6: Beliebiges Viereck

Die zeichnerisch/technische Durchführung gibt mit dem Übertragen der Teilverhältnisse einiges zu tun, ist aber elementar.

Im Sonderfall eines Parallelogramms ABCD liefert die Konstruktion die Diagonale AC.

4.1 Beweis mit Vektorrechnung

Wir bezeichnen mit den Ortsvektor des Punktes X. Den Punkt A setzen wir in den Ursprung, also . Das mehrfach vorkommende Teilverhältnis bezeichnen wir mit t. Mit diesen Bezeichnungen ist:

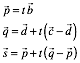
Einsetzen liefert:

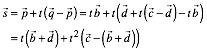
Mit den Bezeichnungen und erhalten wir:

Im Koordinatensystem mit den Einheitsvektoren und ist dies die Standardparabel, in der ursprünglichen Situation also das affin verzerrte Bild der Standardparabel. Da eine affine Abbildung parabeltreu ist, haben wir auch in der ursprünglichen Situation eine Parabel. Die Abbildung 7 zeigt die Situation der Vektoren und .

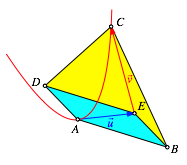
Abb. 7: Die beiden Vektoren

Der Vektor gibt die Abweichung des Viereckes vom Parallelogramm. Für , also den Fall eines Parallelogramms, ergibt sich die Diagonale AC.

Wenn und linear abhängig sind (Abb. 8), ergibt sich ebenfalls die Diagonale AC. In diesem Fall ist das Viereck ABCD ein affin verzerrtes Drachenviereck. In einem Drachenviereck ergibt sich aber aus Symmetriegründen die Diagonale.

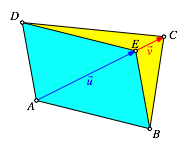
Abb. 8: Affin verzerrter Drachen

4.2 Beweis mit Koordinatenrechnung

Im allgemeinen Fall mit linear unabhängigen Vektoren und können wir durch eine affine Verzerrung folgende Situation erreichen. Der Punkt A wird zum Ursprung, der Punkt E der Abbildung 8 zum Einheitspunkt auf der x-Achse und der Punkt C zum Punkt (Abb. 9). Dem verzerrten Punkt B ordnen wir die Koordinaten zu. Der Punkt D hat dann die Koordinaten .

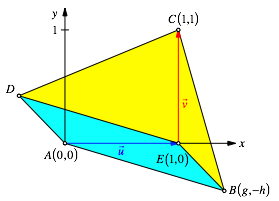
Abb. 9: Affin verzerrte Situation

Das Teilverhältnis bezeichnen wir wiederum mit t. Damit erhalten wir für den Punkt P die Koordinaten , für den Punkt Q die Koordinaten und schließlich für den Punkt S die Koordinaten . Dies beschreibt aber die Standardparabel. Daher beschreibt S auch vor der affinen Verzerrung eine Parabel.