Hans Walser, [20210531], [20210607]
Paraboloid-Stern
1 Worum geht es?
Der Paraboloid-Stern, das Rhombendodekaeder, das Oktaeder und das Oktaeder mit dualem Wrfel haben in allen drei Rissen dieselbe Kontur.
2 Paraboloid
2.1 Definition
Das einschalige Paraboloid (Abb. 1 und 2) ist der Funktionsgraf von
![]() (1)
(1)
bei gleicher Skalierung auf allen drei Koordinatenachsen.

Abb. 1: Paraboloid
Man beachte, dass die positive x-Achse nach rechts vorne und die positive y-Achse nach rechts hinten verlaufen.

Abb. 2: Paraboloid
Fr das Paraboloid erhalten wir das Volumen:
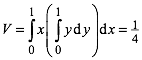 (2)
(2)
2.2 Ebene Schnitte
Senkrechte Schnitte parallel zur x-Achse sind Geraden (Abb. 3). Wir haben also eine Geradenschar. Die Flche ist eine Regelflche. Ihre Gau§sche Flchenkrmmung ist negativ. Die Flche kann daher nicht in die Ebene abgewickelt werden.
Aus Symmetriegrnden gibt es noch eine zweite Geradenschar auf der Flche, nmlich die senkrechten Schnitte parallel zur y-Achse.

Abb. 3: Senkrechte Schnitte
2.3 Niveaulinien
Die Niveaulinien sind gleichseitige Hyperbeln (Abb. 4 und 5).
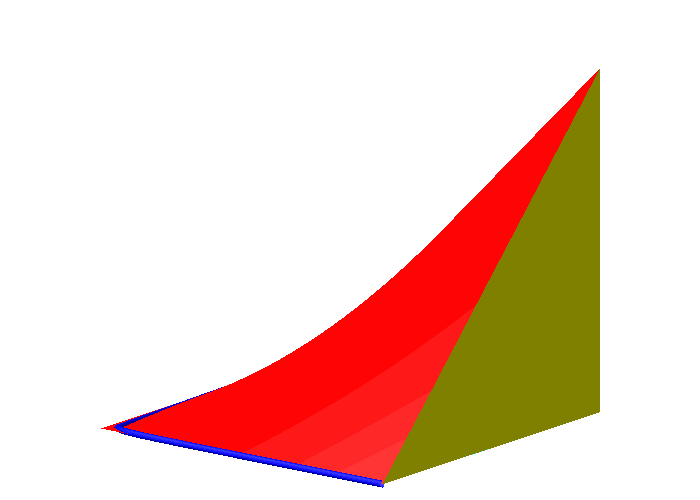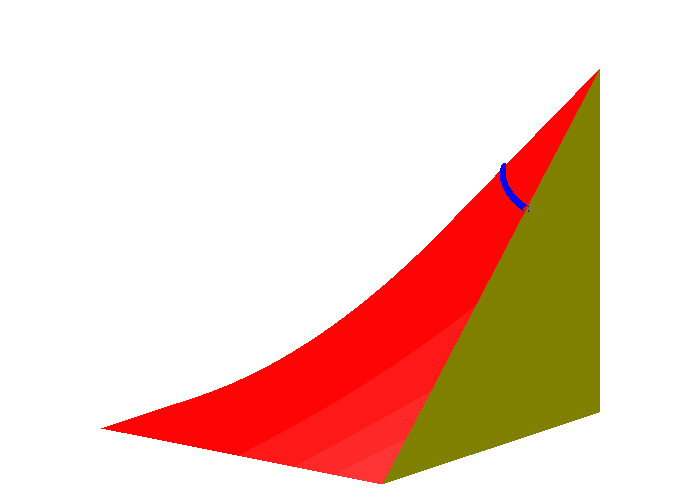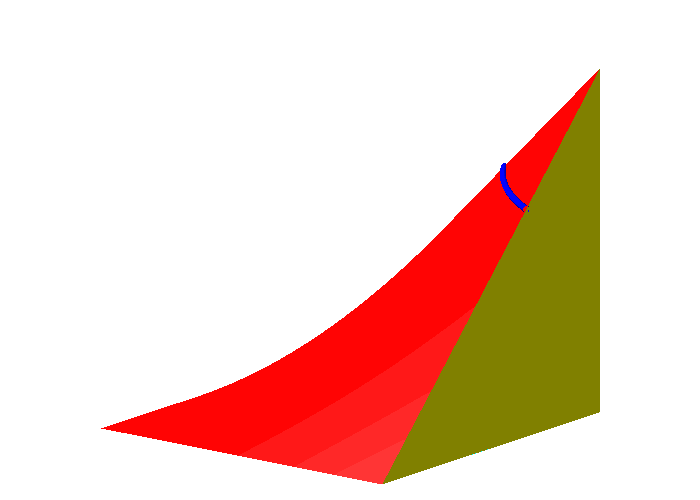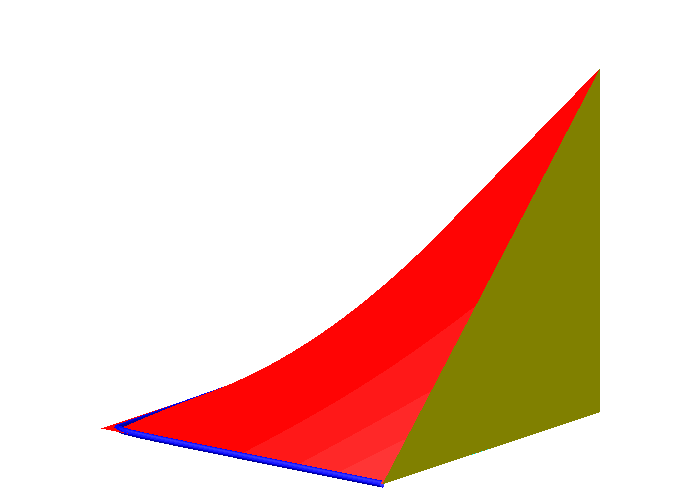
Abb. 4: Niveaulinien

Abb. 5: Sicht von oben
2.4 Risse
Die Abbildung 6 gibt Grund-, Auf- und Seitenriss des Paraboloides der Abbildung 1.
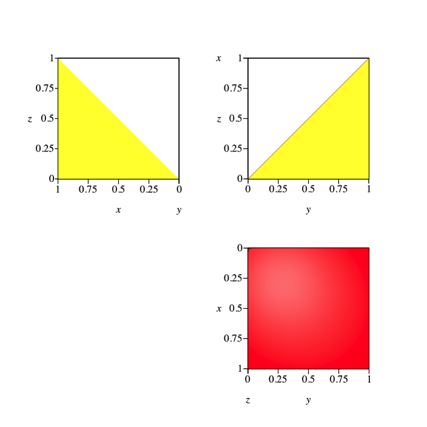
Abb. 6: Risse
3 Eine schiefe Pyramide
Die schiefe Pyramide der Abbildungen 7 und 8 hat dieselben Eckpunkte wie der in der Abbildung 1 gegebene Krper. Sie hat eine quadratische Grundflche und die Spitze senkrecht ber einer Quadratecke.
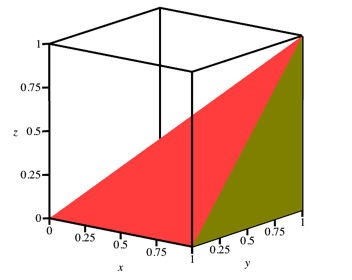
Abb. 7: Schiefe Pyramide
Die Pyramide fllt volumenm§ig genau einen Drittel des in der Abbildung 7 eingezeichneten Koordinatenwrfels. Dies kann wie folgt eingesehen werden:
Geometrische berlegung: Wir knnen je eine Pyramide mit dem Einheitsquadrat in der x,y-Ebene (Abb. 7), in der y,z-Ebene und in der zx-Ebene bauen. Diese drei Pyramiden fllen den Einheitswrfel lckenlos und berlappungsfrei.
Rechnung: Die Niveauflchen der Pyramide der Abbildung 7 auf der Hhe z sind Quadrate mit der Seitenlnge (1 – z). Daher ergibt sich das Volumen:
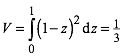 (3)
(3)

Abb. 8: Schiefe Pyramide
Die drei Risse (Abb. 9) haben dieselben Konturen wie die Risse der Abbildung 6.
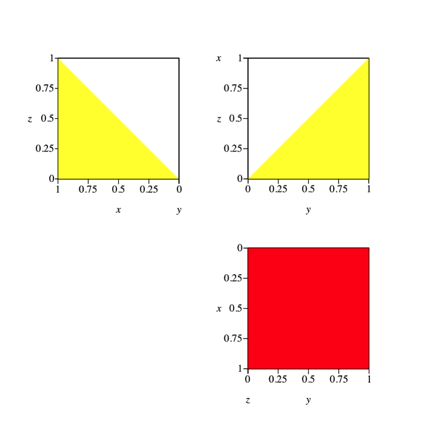
Abb. 9: Risse
4 Zusammensetzungen
4.1 Vier Paraboloide
Wir setzen vier Paraboloide der Abbildung 1 zusammen (Abb. 10 und 11).
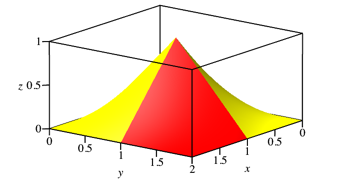
Abb. 10: Vier Paraboloide
Wegen (2) haben diese vier Paraboloide zusammen das Volumen 1.

Abb. 11: Vier Paraboloide
Die Abbildung 12 zeigt die drei Risse.
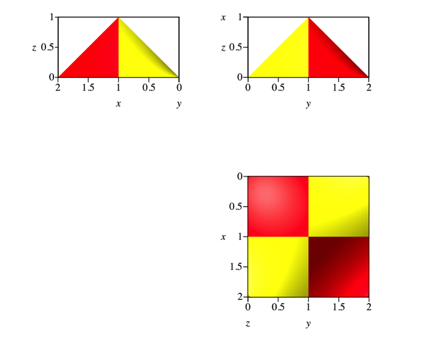
Abb. 12: Risse
4.2 Vier schiefe Pyramiden
Nun machen wir dasselbe Spielchen mit schiefen Pyramiden der Abbildung 7. Wir erhalten eine gerade Pyramide (Abb. 13 und 14).
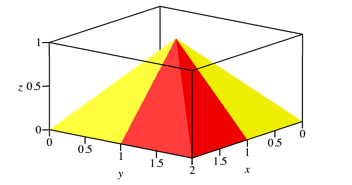
Abb. 13: Pyramide
Wegen (3)
hat diese Pyramide das Volumen ![]() .
.

Abb. 14: Pyramide
Diese Pyramide ist ein alter Bekannter. Wir knnen einen Wrfel vom Mittelpunkt aus in sechs Pyramiden er Abbildung 13 zerlegen (Abb. 15). Die Hhe der Pyramide ist daher halb so gro§ wie die Kantenlnge am Boden. Die Seitenflchen haben gegenber dem Boden einen Neigungswinkel 45¡.
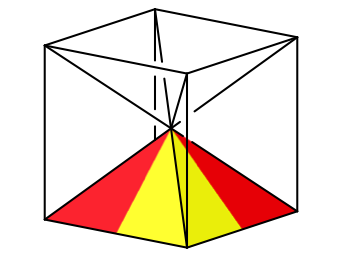
Abb. 15: Pyramide im Wrfel
Die Abbildung 16 gibt die Risse der Pyramide.
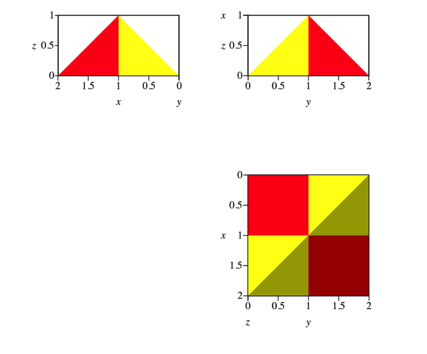
Abb. 16: Risse
Wir sehen die gleichen Konturen wie bei der Abbildung 12.
5 Auf dem Wrfel
5.1 Paraboloid
Wir knnen die vier Paraboloide der Abbildung 10 auf einen Wrfel setzen (Abb. 17).

Abb. 17: Auf dem Wrfel
Natrlich knnen wir auf allen sechs Seiten des Wrfels vier Paraboloide ansetzen. Dies ergibt den Paraboloid-Stern (Abb. 18 und 19). Er hat 14 Spitzen.
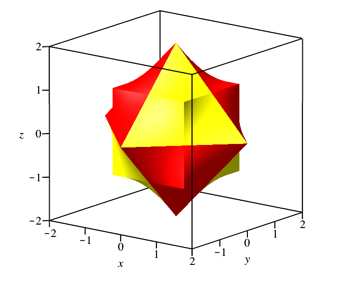
Abb. 18: Paraboloid-Stern
Das Volumen des Paraboloid-Sterns setzt sich aus den Volumina des Wrfels und der angesetzten Pyramiden zusammen. Wegen (2) ergibt sich das Gesamtvolumen 14.

Abb. 19: Paraboloid-Stern
Die Abbildung 20 zeigt die drei Risse. Worin unterscheiden sich die drei Risse?
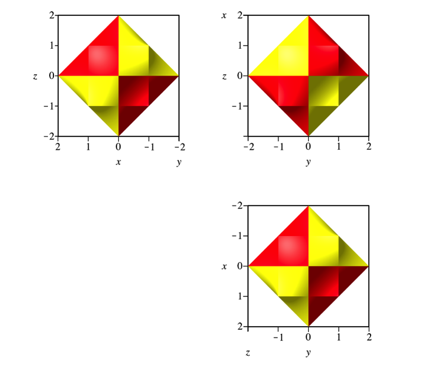
Abb. 20: Risse
5.2 Rhombendodekaeder
Dasselbe Spielchen mit der Pyramide der Abbildung 13 gibt das sogenannte Rhombendodekaeder (Abb. 21 und 22). Die zwlf Seitenflchen sind Rhomben, in unserem Beispiel durch die lange Diagonale farblich zweigeteilt. Das Rhombendodekaeder ist die konvexe Hlle des Paraboloid-Sternes.
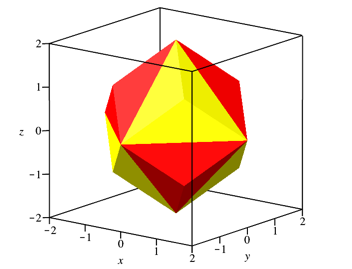
Abb. 21: Rhombendodekaeder
Wegen (3) ist das Gesamtvolumen 16, also das Doppelte des Wrfelvolumens.

Abb. 22: Rhombendodekaeder
Die Abbildung 23 zeigt die drei Risse. Wegen der offenbar nicht optimalen Beleuchtung sind nicht alle Binnenkanten erkennbar.
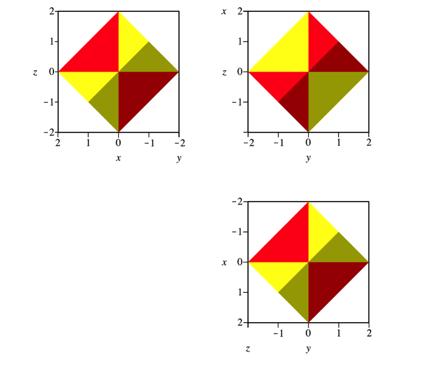
Abb. 23: Risse
Wir haben dieselben Konturen wie in der Abbildung 20.
6 Weitere Beispiele
6.1 Oktaeder
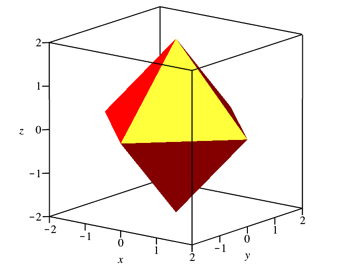
Abb. 24: Oktaeder

Abb. 25: Oktaeder
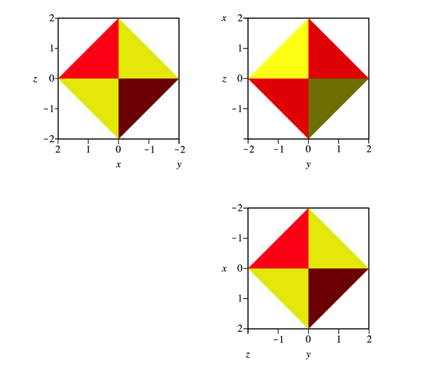
Abb. 26: Risse
6.2 Oktaeder mit dualem Wrfel
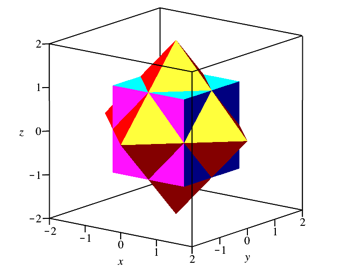
Abb. 27: Oktaeder mit dualem Wrfel

Abb. 28: Oktaeder mit dualem Wrfel
Das Oktaeder mit dualem Wrfel hat als konvexe Hlle das Rhombendodekaeder.
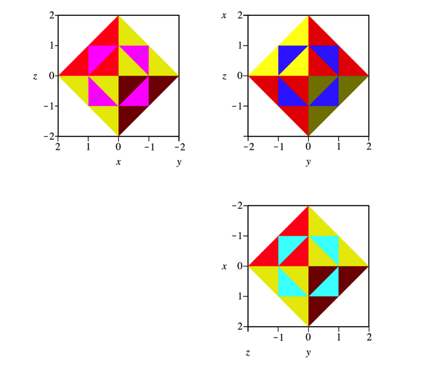
Abb. 29: Risse
Die Risse der Abbildungen 20 (Paraboloid-Stern), 23 (Rhombendodekaeder), 26 (Oktaeder) und 29 (Oktaeder mit dualem Wrfel) haben alle dieselben Konturen.
Websites
Hans-Jrgen Elschenbroich: Konoid
https://www.geogebra.org/m/y57fhddh
Hans-Jrgen Elschenbroich: Konoid 2
https://www.geogebra.org/m/gqfnnhfe
Hans-Jrgen Elschenbroich: Konoidmantel
https://www.geogebra.org/m/y57fhddh
Hans Walser: Dreitafelprojektion
http://www.walser-h-m.ch/hans/Miniaturen/D/Dreitafelprojektion/Dreitafelprojektion.htm
Hans Walser: Hyperboloid-Stern
http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperboloid-Stern/Hyperboloid-Stern.htm
Hans Walser: Pyramidoid
http://www.walser-h-m.ch/hans/Miniaturen/P/Pyramidoid/Pyramidoid.htm
Hans Walser: Rohrpost
http://www.walser-h-m.ch/hans/Miniaturen/R/Rohrpost/Rohrpost.htm
Hans Walser: Sphroid
http://www.walser-h-m.ch/hans/Miniaturen/S/Sphaeroid/Sphaeroid.htm