1 Worum geht es?

Anhand eines räumlichen Hyperbolischen Paraboloid-Modells wird die Ableitung der Quadratfunktion hergeleitet.

2 Das hyperbolische Paraboloid

Beat lernt in der Schule, dass durch die Gleichung ein hyperbolisches Paraboloid beschrieben wird (Abb. 1).

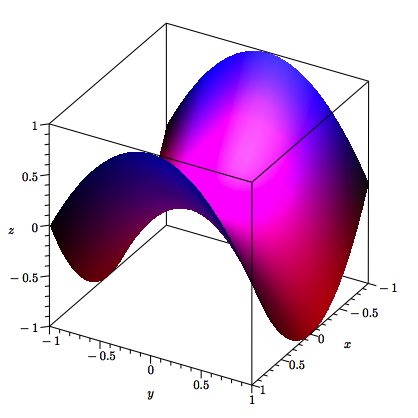
Abb. 1: Hyperbolisches Paraboloid

3 Parabeln als Konturlinien

Sofort sieht er, dass es in der Ebene eine nach oben offene Parabel gibt (Abb. 2). Die Parabel hat die Gleichungen .

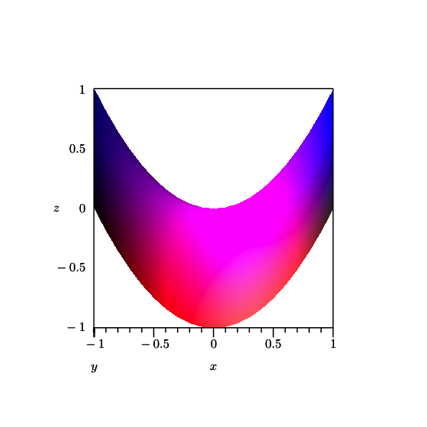
Abb. 2: Konturparabel

Entsprechend gibt es eine nach unten offene Parabel mit den Gleichungen und 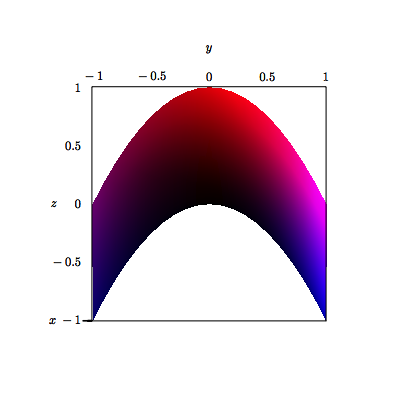(Abb. 3).

Abb. 3: Untere Konturparabel

In der Abbildung 4 sind die beiden Parabeln schwarz eingezeichnet.

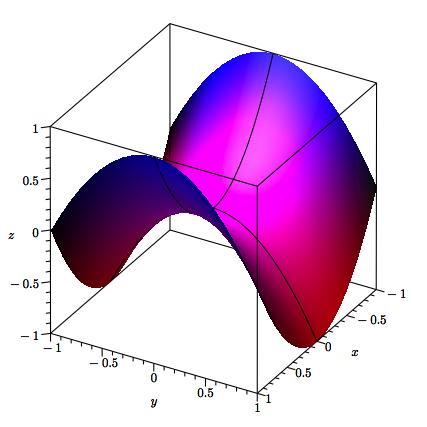
Abb. 4: Die beiden Parabeln

4 Das Modell

Nun denkt sich Beat folgendes Modell aus: Er biegt zwei Lochstreifen parabelförmig und schraubt sie in der Mitte orthogonal zusammen so dass eine Parabel nach oben und die andere nach unten offen ist. Dann verbindet er mit Bindfäden (Abb. 5).

Abb. 5: Modell von Beat

Die Abbildung 6 zeigt einen elektronischen Nachbau des Modells.

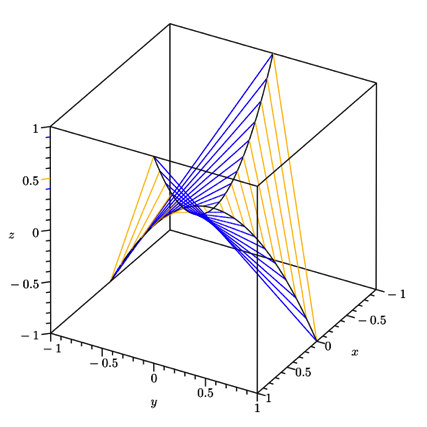
Abb. 6: Modell von Beat

5 Die Ableitung

Die Abbildung 7 zeigt wiederum die obere Profilparabel.

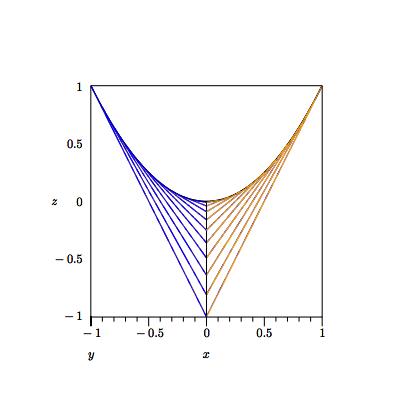
Abb. 7: Profilparabel

Nun interpretiert Beat die Figur zweidimensional in einem x,z-Koordinatensystem. Die blauen und gelben Bindfäden sind offensichtlich Tangenten an die Parabel . Die Tangente im Berührpunkt schneidet die z-Achse aus Symmetriegründen im Punkt . Sie hat also die Steigung . Daraus ergibt sich, dass die Funktion die Ableitung hat.