1 Das Einstiegsbeispiel

Ein HIV-Test reagiert bei HIV-positiven Personen mit 90% Wahrscheinlichkeit positiv. Bei HIV-negativen Personen gibt er mit 5% Wahrscheinlichkeit irrtümlicherweise auch ein positives Resultat.

Das Testverfahren geht nun so vor sich, dass zunächst jede Person mit diesem Test getestet wird. Da es bekanntlich in denjenigen Fällen mit einem positiven Testresultat viele „Fehlalarme“ hat, wird bei positivem Testresultat der Test wiederholt.

Es werden 1'000'000 Personen getestet. Dabei haben 134'930 Personen auch beim zweiten Test ein positives Testresultat.

Welcher Anteil der getesteten Personen ist tatsächlich HIV-positiv?

2 Bearbeitung

Es sei x der zu schätzende Anteil der tatsächlich HIV-positiven Personen.

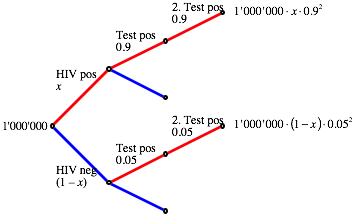
Baum

Aus der Baumdarstellung lesen wir ab:

Daraus ergibt sich . Der gesuchte Anteil ist 16.4%, also etwa 164'000 Personen. Wir haben eine Dunkelziffer.

Und nun das Paradoxon: Wenn der Test bei zweimal positivem Testresultat ein drittes Mal wiederholt wird, ergibt sich die Gleichung

mit der Lösung . Die Dunkelziffer wird größer.

Wir bezeichnen mit die Lösung der Gleichung

Die Tabelle zeigt die Lösungen.


1	0.099918
2	0.164
3	0.18495
4	0.20565
5	0.2285
6	0.25389
7	0.28211
8	0.31345
9	0.34828
10	0.38698
11	0.42997
12	0.47775
13	0.53083
14	0.58981
15	0.65535
16	0.72816
17	0.80907
18	0.89897
19	0.99885
20	1.1098

Wir sehen, dass für der Anteil der tatsächlich HIV-positiven Personen die 100%-Grenze übersteigt.

Der „Hund“ liegt darin, dass wir immer mit derselben Anzahl von 134'930 Personen gerechnet haben, welche nach mehrfach positivem Testergebnis weiter getestet wurden.

3 Mehrfaches Testen

Wir sehen nun die Sache in umgekehrter Richtung an und gehen davon aus, dass 100'000 Personen tatsächlich HIV-positiv seien. Bei einmaligem Testen ist die Wahrscheinlichkeit, dass eine Person mit positivem Testresultat tatsächlich HIV-positiv ist, gegeben durch die bedingte Wahrscheinlichkeit:

Wir haben also einen Drittel Fehlalarme. Wir hingegen bei positivem Testresultat der Test wiederholt, ergibt sich:

Die Fehlalarmquote ist nur noch etwa 3%. Sie tendiert bei weiteren Testwiederholungen gegen Null.

Allerdings werden bei jeder Testwiederholung tatsächlich HIV-positive Personen aus der Berechnung ausgeschieden.

n	Noch zu testende Personen	HIV-positiv	HIV-negativ	Bedingte Wahrscheinlichkeit
1	135000	90000	45000	0.6666666667
2	83250	81000	2250	0.972972973
3	73012	72900	112	0.9984660056
4	65616	65610	6	0.9999085589
5	59049	59049	0	1.0
6	53144	53144	0	1.0
7	47830	47830	0	1.0
8	43047	43047	0	1.0
9	38742	38742	0	1.0
10	34868	34868	0	1.0
11	31381	31381	0	1.0
12	28243	28243	0	1.0
13	25419	25419	0	1.0
14	22877	22877	0	1.0
15	20589	20589	0	1.0
16	18530	18530	0	1.0
17	16677	16677	0	1.0
18	15009	15009	0	1.0
19	13509	13509	0	1.0
20	12158	12158	0	1.0