1 Worum es geht

Geometrische Spielerei im Parallelogramm. Diagonalen und Höhen.

Resultate mit DGS verifiziert, um formale Beweise bin ich dankbar.

2 Quadrate ansetzen

Einem Parallelogramm setzen wir auf den Seiten Quadrate an (Abb. 1).

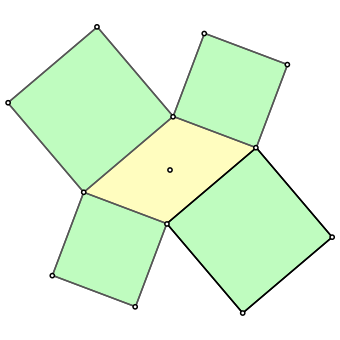
Abb. 1: Quadrate ansetzen

3 Zwei weitere Parallelogramme

Nun verbinden wir die vier vom Mittelpunkt aus gesehen jeweils linken äußeren Quadratecken (rot in Abb. 2). Das entstehende Viereck ist aus Symmetriegründen wieder ein Parallelogramm.

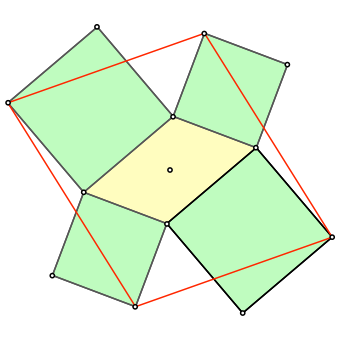
Abb. 2: Rotes Parallelogramm

Analog verbinden wir die jeweils rechten äußeren Quadratecken (blau in Abb. 3). Man kann zeigen, dass die beiden Parallelogramme denselben Flächeninhalt haben (Rechnung in ℂ).

Die beiden Parallelogramme haben acht Schnittpunkte, welche paarweise punktsymmetrisch zum Mittelpunkt liegen. Die Punkte sind im Wechsel magenta und lila gezeichnet.

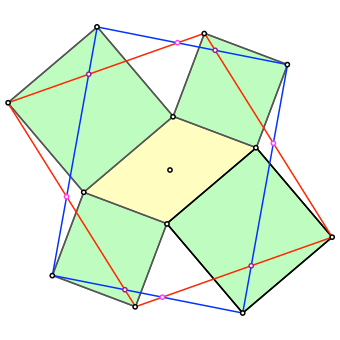
Abb. 3: Blaues Parallelogramm

4 Diagonalen

Die magenta Schnittpunkte liegen auf den Diagonalen des Startparallelogramms (Abb. 4).

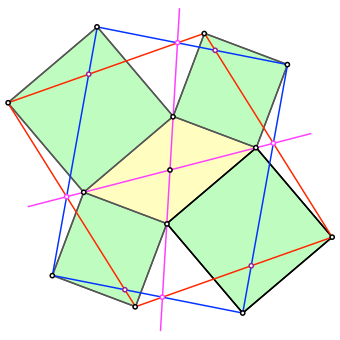
Abb. 4: Diagonalen

5 Höhen

Die lila Schnittpunkte liegen auf den verlängerten Höhen des Startparallelogramms durch den Mittelpunkt (Abb. 5).

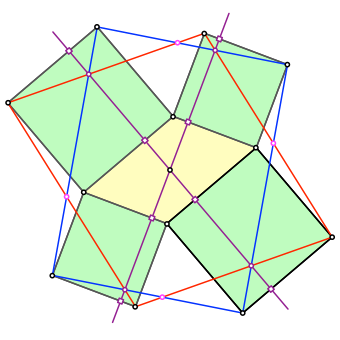
Abb. 5: Höhen

6 Übersicht

Die Abbildung 6 zeigt die integrale Figur.

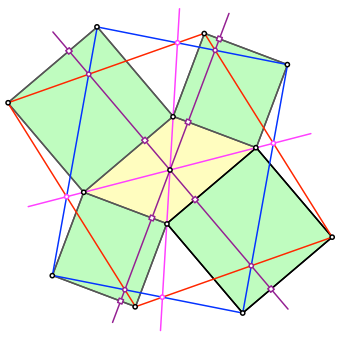
Abb. 6: Diagonalen und Höhen