Hans Walser, [20220526]
Parkett
Idee und Anregung: Maik Bleckmann, Bremen
Inhalt
4.2 Flächeninhalt des regelmäßigen Zwölfeckes
1 Worum geht es?
Beispiele von Parketten.
Frage der Periodizität.
2 Fliesen
Die Fliesen sind (weitgehend) aus gleichseitigen und rechtwinklig-gleichschenkligen Dreiecken (Abb. 1) zusammengesetzt.
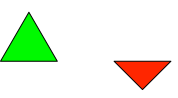
Abb. 1: Basisdreiecke
Die beiden Dreiecke setzen wir zu einem Drachenviereck zusammen (Abb. 2).
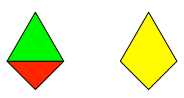
Abb. 2: Drachenviereck
Ein Malteserkreuz wird mit Rhomben ergänzt (Abb. 3).
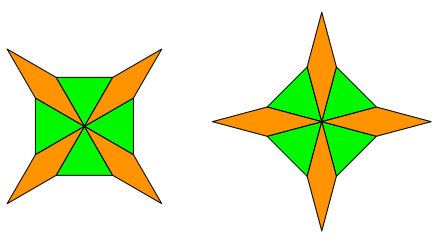
Abb. 3: Rhomben
Ein gleichseitiges Dreieck und ein rechtwinklig gleichschenkliges können auch asymmetrisch zusammengesetzt werden (Abb. 4). Die hellblaue und die magenta Fliese, zusammengesetzt je aus einem gleichseitigen Dreieck (schwarz) und einem rechtwinklige gleichschenkligen Dreieck (rot) sind asymmetrisch. Sie sind zueinander ungleichsinnig kongruent.
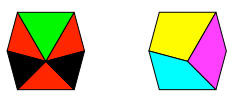
Abb. 4: Asymmetrische Fliesen
Alle Fliesenwinkel in den Abbildungen 1 bis 4 sind Vielfache von 15°.
3 Drachen
Wir setzen Drachenvierecke und rechtwinklig gleichschenklige Fliesen zusammen gemäß Abbildung 5.
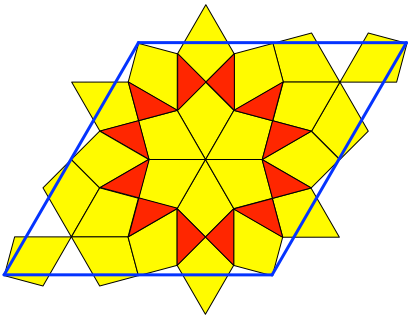
Abb. 5: Mit Drachenvierecken
Die Figur passt in einen 60°-Rhombus (blau). Was auf einer Seite vorsteht, fehlt auf der gegenüberliegenden Seite. Die Figur und der Rhombus haben daher denselben Flächeninhalt.
Wir können die Rhomben mitsamt den Figuren bündig zusammensetzen (Abb. 6).
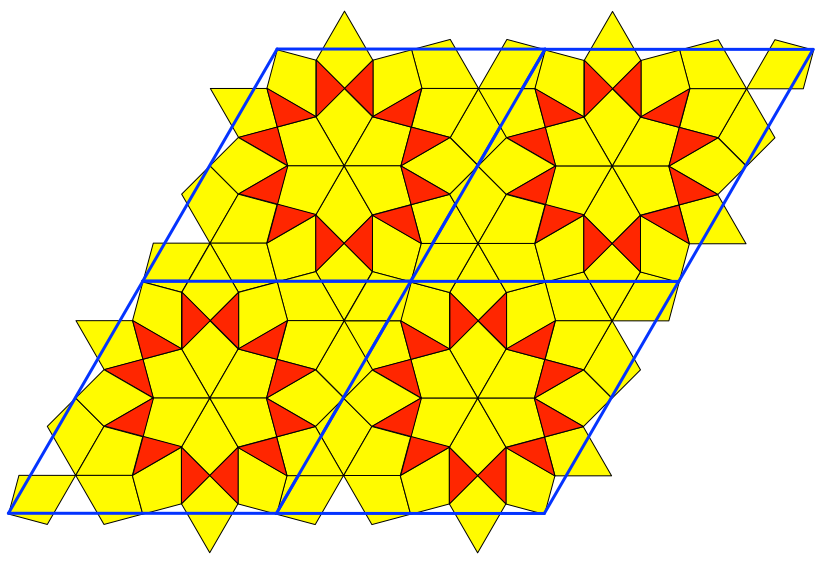
Abb. 6: Zusammensetzung
Es entsteht ein periodisches Parkett (Abb. 7). Der Rhombus ist der Periodizitätsbereich. Das Parkett hat dieselben Symmetrien wie das Bienenwabenmuster.

Abb. 7: Parkett
Wir können das Drachenviereck wieder auflösen in ein gleichseitiges und ein rechtwinklig gleichschenkliges Dreieck gemäß Abbildung 2. Statt der Abbildung 5 erhalten wir dann die Figur der Abbildung 8.
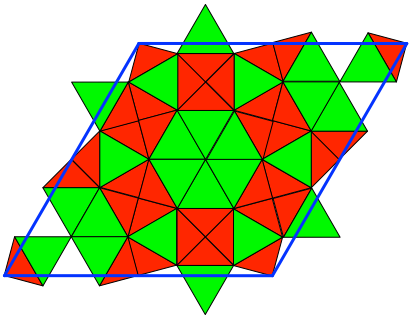
Abb. 8: Zerlegung des Drachenviereckes
Die Abbildung 9 zeigt das zugehörige Parkett. Es besteht farblich gesehen aus Dreiecken, Quadraten und Sechsecken.

Abb. 9: Parkett
Die beiden Verfahren sind kompatibel. Die Abbildung 10 zeigt eine Hybridlösung.

Abb. 10: Hybridlösung
4 Rhomben
Wir stellen die Fliesen der Abbildung 3 um gemäß Abbildung 11.
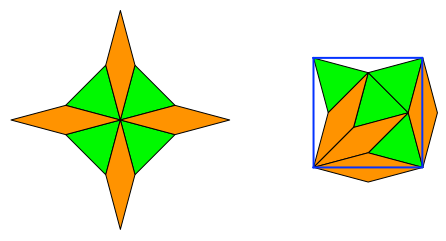
Abb. 11: Umstellen der Fliesen
Nun passt die Figur in ein flächengleiches Quadrat. Wir können damit ein periodisches Parkett bauen (Abb. 12). Es kann in allen Richtungen beliebig weit periodisch fortgesetzt werden.
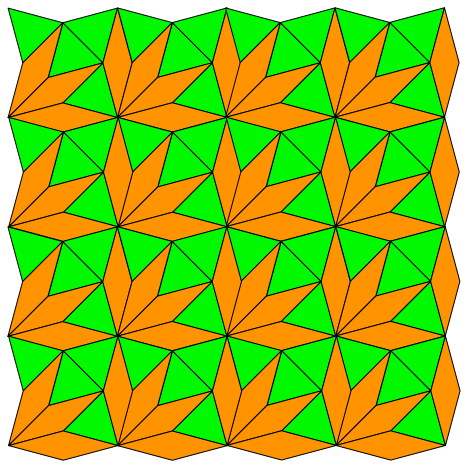
Abb. 12: Periodisches Parkett
Allerdings können wir auch eine Quadrantenfigur bauen (Abb. 13). Wir haben im Zentrum einen Stern mit zwölf Spitzen, der sonst nirgends mehr erscheint.

Abb. 13: Vier Quadranten
Auch diese Figur kann in allen Richtungen beliebig weit fortgesetzt werden. Sie ist aber nicht mehr periodisch.
Hingegen können wir mit derselben Quadrantenidee auch ein periodisches Parkett bauen (Abb. 14).

Abb. 14: Periodisch
4.1 Aperiodische Parkette
Das Beispiel der Abbildung 13 ist zwar aperiodisch. Es gehört aber nicht zu den zwangsweise aperiodischen Parketten etwa von Roger Penrose. Bei den Penrose-Parketten bestehen zusätzliche Anlegevorschriften, zum Beispiel Farbcodes an den Ecken oder Kanten. Diese Anlegevorschriften verhindern periodische Anordnungen.
4.2 Flächeninhalt des regelmäßigen Zwölfeckes
Das regelmäßige Zwölfeck mit dem Umkreisradius 1 hat den Flächeninhalt 3. Dies kann durch die Zerlegung gemäß Abbildung 15 eingesehen werden.
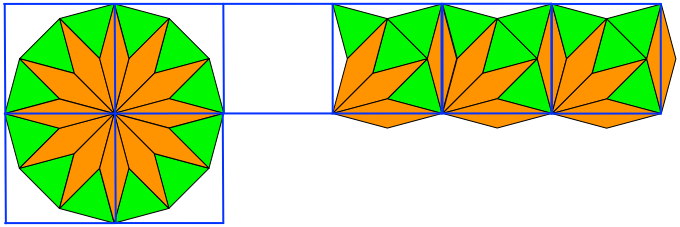
Abb. 15: Zwölfeck
5 Asymmetrische Fliesen
Mit den asymmetrischen Fliesen der Abbildung 4 kann zunächst ein periodisches Parkett gebaut werden (Abb. 16).
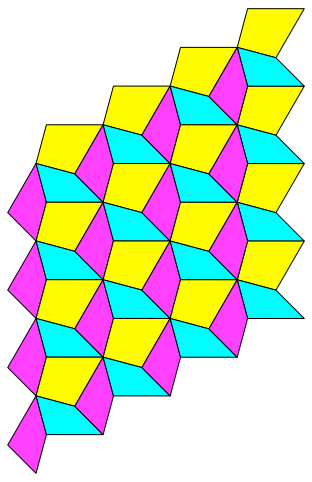
Abb. 16: Periodisches Parkett mit asymmetrischen Fliesen
Es gibt aber auch eine aperiodische Sextantenlösung (Abb. 17).

Abb. 17: Aperiodische Lösung
Eine nachträgliche Periodisierung (Abb. 18) verlangt den Einbau von zusätzlichen kleinen schwarzen gleichseitigen Dreiecken der Abbildung 4.

Abb. 18: Periodisches Parkett
Literatur
Bleckmann, Maik (2022): Pyramidenansatz zum Erstellen von Mustern (Manuskript)
Weblink
Hans Walser: Zwölfecksfläche
http://www.walser-h-m.ch/hans/Miniaturen/Z/Zwoelfecksflaeche/Zwoelfecksflaeche.htm