Hans Walser, [20191211]
Pascal und Fibonacci
1 Worum geht es?
Verallgemeinerte Fibonacci-Folgen auf der Basis von Potenzen der Pascal-Matrix.
2 Erinnerungen
Wenn wir im Pascal-Dreieck der Binomialkoeffizienten die Schrgzeilensummen bilden gem§ Abbildung 1 erhalten wir die Fibonacci-Zahlen.
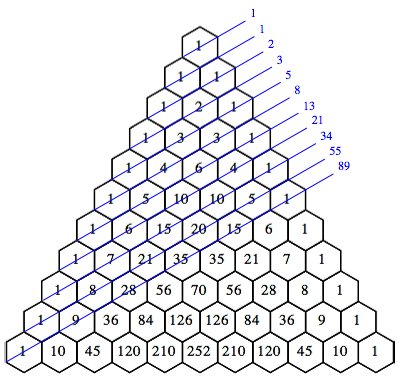
Abb. 1: Schrgzeilensummen
Die
Fibonacci-Zahlen ![]() haben mit
den Startwerten
haben mit
den Startwerten ![]() die
Rekursion:
die
Rekursion:
![]() (1)
(1)
Weiter gilt der Grenzwert:
![]() (2)
(2)
Der Grenzwert ist der Goldene Schnitt (Walser 2013). Er ist die positive Lsung der quadratischen Gleichung:
![]() (3)
(3)
3 Pascal-Matrix
Das Pascal-Dreieck kann auch in eine Dreiecksmatrix eingekastelt werden (Abb. 2).
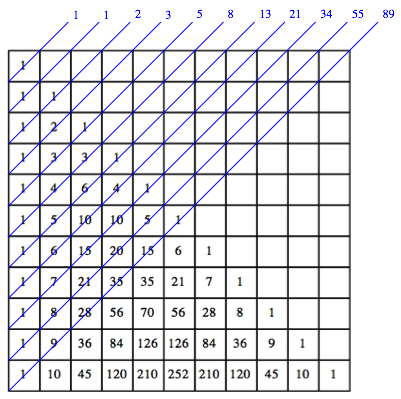
Abb. 2: Pascal-Matrix
Die Schrgzeilen erscheinen jetzt als Diagonalen.
4 Quadrat der Pascal-Matrix
Wir multiplizieren die Pascal-Matrix mit sich selbst im Sinne der Matrizenmultiplikation. Das Resultat ist wieder eine Dreiecksmatrix (Abb. 3).
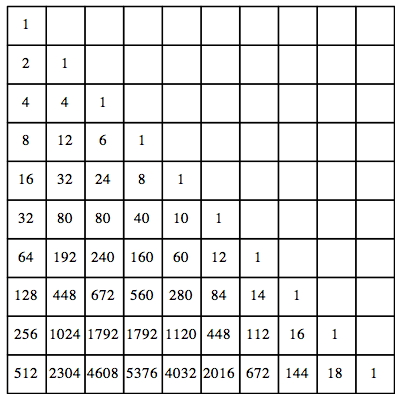
Abb. 3: Quadrat der Pascal-Matrix
Die Folge der Schrgzeilensummen ist:
|
1 |
2 |
5 |
12 |
29 |
70 |
169 |
408 |
985 |
2378 |
Die Folge
hat mit den Startwerten ![]() die
Rekursion:
die
Rekursion:
![]() (4)
(4)
Weiter ist:
![]() (5)
(5)
Dies ist die positive Lsung der quadratischen Gleichung:
![]() (6)
(6)
5 Dritte Potenz der Pascal-Matrix
Fr die dritte Potenz der Pascal-Matrix erhalten wir (Abb. 4):
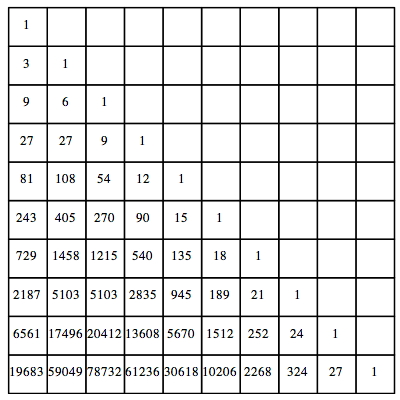
Abb. 4: Dritte Potenz der Pascal-Matrix
Die Folge der Schrgzeilensummen ist:
|
1 |
3 |
10 |
33 |
109 |
360 |
1189 |
3927 |
12970 |
42837 |
Die Folge
hat mit den Startwerten ![]() die
Rekursion:
die
Rekursion:
![]() (7)
(7)
Weiter ist:
![]() (8)
(8)
Dies ist die positive Lsung der quadratischen Gleichung:
![]() (9)
(9)
6 Allgemein
Fr die n-te Potenz der Pascal-Matrix ergibt
sich die Schrgzeilen-Summenfolge mit den Startwerten ![]() und der
Rekursion:
und der
Rekursion:
![]() (10)
(10)
Weiter ist:
![]() (11)
(11)
Dies ist die positive Lsung der quadratischen Gleichung:
![]() (12)
(12)
7 Inverse
Fr die Inverse der Pascal-Matrix erhalten wir (Abb. 5):
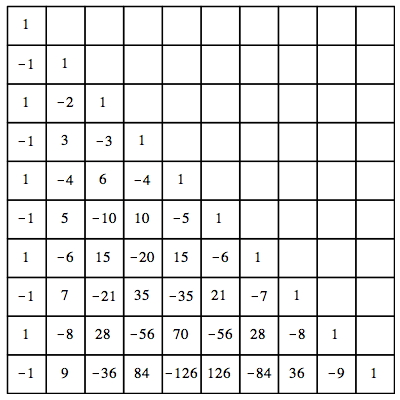
Abb. 5: Inverse der Pascal-Matrix
Dies ist die Pascal-Matrix mit alternierenden Vorzeichen. Die Schrgzeilensummen haben daher bei gleichen Betrgen ebenfalls alternierende Vorzeichen. Analoges gilt fr weitere Potenzen mit negativen Exponenten.
Literatur
Walser, H. (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.