Hans Walser, [20150426]
Pascal-Dreieck variiert
1 Standard
Wir codieren die EintrŠge im Pascalschen Dreieck der Binomialkoeffizienten farblich gemŠ§ ParitŠt: rot fźr gerade und blau fźr ungerade (Abb. 1). Au§erhalb des Dreieckes sei rot. Das Spitzenfeld setzen wir blau.
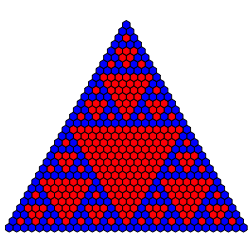
Abb. 1: Farbcodierung
Die Rekursionsformel der Binomialkoeffizienten kann in dieser Farbcodierung auf vier FŠlle gemŠ§ Abbildung 2 reduziert werden.
Abb. 2: Farbrekursion
Die beiden Farben links und rechts oberhalb des Feldes definieren die Farbe des Feldes.
2 Variation der Farbrekursion
Wir
codieren die Farben mit 0 fźr gerade und 1 fźr ungerade. Die Farbrekursion ist
also eine Funktion 
von zwei Variablen, welche je den Wert 0
oder 1 haben kšnnen. Dabei stehen x
fźr die Farbe im Feld oben links und y
fźr die Farbe im Feld oben rechts. Wir haben vier mšgliche Inputkombinationen.
Da als output ebenfalls nur 0 oder 1 in Frage kommen, ergeben sich 
mšgliche Farbrekursionen. Diese sind in
der Tabelle 1 aufgelistet. Die Kopfzeile enthŠlt die vier Inputkombinationen.
Jede Zeile im Tabellenkšrper gibt eine Outputkombination. Die letzte Spalte
gibt eine dazu passende Funktion.
|
0,0 |
0,1 |
1,0 |
1,1 |
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
|
|
0 |
1 |
0 |
1 |
|
|
0 |
1 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
|
|
1 |
0 |
1 |
0 |
|
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
0 |
|
|
1 |
1 |
0 |
1 |
|
|
1 |
1 |
1 |
0 |
|
|
1 |
1 |
1 |
1 |
1 |
Tab. 1: Farbrekursionen
Das Beispiel der Abbildung 2 gehšrt zur Outputkombination (0,1,1,0).
3 Variation der Dreiecke
Es werden die 16 Beispiele durchexerziert, wobei Beispiele mit gleichem Bild zusammengefasst werden. Verschiedene Beispiele sind eher langweilig.
3.1 Blaue Spitze
Die Outputkombinationen (0,0,0,0), (0,0,0,1) ergeben je das Beispiel der Abbildung 3. Wir sehen viel rot.
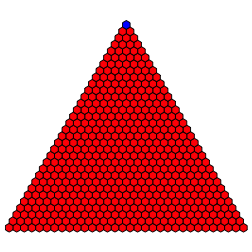
Abb. 3: (0,0,0,0), (0,0,0,1)
3.2 Blaue SchrŠge rechts
Die Outputkombinationen (0,0,1,0), (0,0,1,1) ergeben je das Beispiel der Abbildung 4.
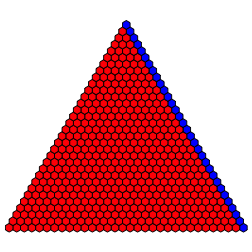
Abb. 4: (0,0,1,0), (0,0,1,1)
3.3 Blaue SchrŠge links
Die Outputkombinationen (0,1,0,0), (0,1,0,1) ergeben je das Beispiel der Abbildung 5.
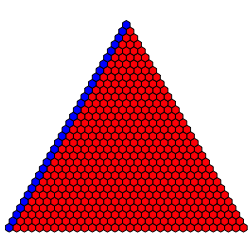
Abb. 5: (0,1,0,0), (0,1,0,1)
3.4 Standard
Die Outputkombination (0,1,1,0) ergibt das schon bekannte Standardbild (Abb. 6).
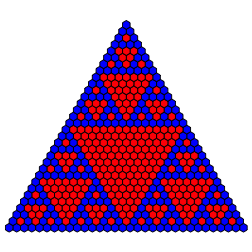
Abb. 6: (0,1,1,0)
3.5 Ganz in Blau
Die Outputkombiantionen (0,1,1,1) und (1,1,1,1) ergibt ein všllig blaues Dreieck (Abb. 7).
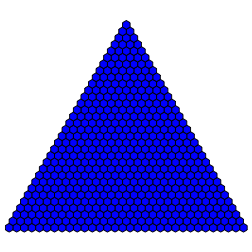
Abb. 7: (0,1,1,1)
3.6 Waagerechte Streifen
Die Outputkombiantion (1,0,0,0) ergibt horizontale Streifen (Abb. 8).
Abb. 8: (1,0,0,0)
3.7 Tausendundeine Nacht
Fźr (1,0,0,1) erhalten wir etwas, das an den Standardfall erinnert (Abb. 9).
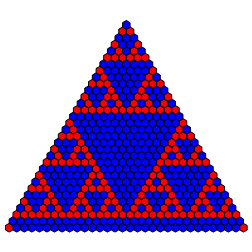
Abb. 9: (1,0,0,1)
3.8 SchrŠge Streifen
Fźr (1,0,1,0) und (1,0,1,1) erhalten wir schrŠge Streifen (Abb. 10).
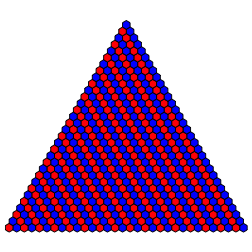
Abb. 10: (1,0,1,0), (1,0,1,1)
Fźr (1,1,0,0) und (1,1,0,1) erhalten wir ebenfalls schrŠge Streifen, aber auf die andere Seite schrŠg (Abb. 11).
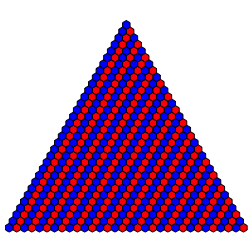
Abb. 11: (1,1,0,0), (1,1,0,1)
3.9 Nochmals horizontale Streifen
Fźr (1,1,1,0) erhalten wir horizontale Streifen in blauem Rahmen (Abb. 12).
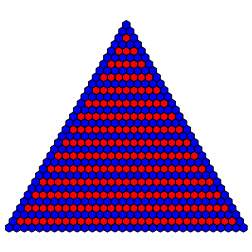
Abb. 12: (1,1,1,0)