Hans Walser, [20210119]
Pascalsche Schnecke und FlŠcheninvarianzen
Anregung: Stephan Berendonk, Kšln
1 Worum geht es?
Ein klassisches Beispiel fŸr eine invariante FlŠchensumme sind die beiden Kathetenquadrate beim rechtwinkligen Dreieck, wenn die Ecke mit dem rechten Winkel auf dem Thaleskreis bewegt wird.
Bei Pascalschen Schnecken gibt es einen Šhnlichen Sachverhalt.
2 Pascalsche Schnecke
Wir arbeiten mit der Polardarstellung (Abb. 1):
(1)
FŸr a = 0 erhalten wir den Einheitskreis.
FŸr 0 < a < 1 ergibt sich eine einfach geschlossene Kurve mit einem Tutsch am linken Rand.
FŸr a = 1 erhalten wir die Kardioide. Sie hat eine EinwŠrtsspitze im Ursprung.
FŸr a > 1 erhalten wir eine Kurve mit einem Doppelpunkt im Ursprung. Die Kurve hat eine Schleife.
SŠmtliche Kurven schneiden die y-Achse bei ±1.
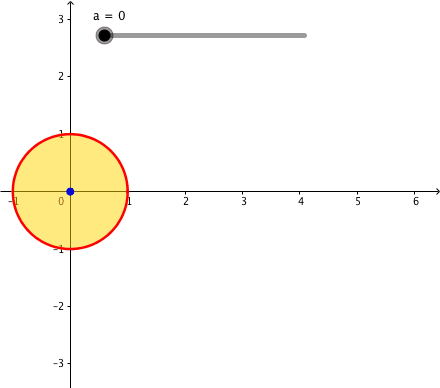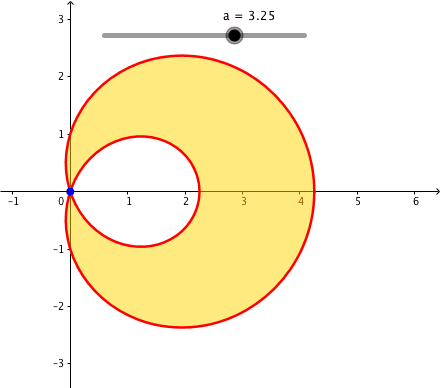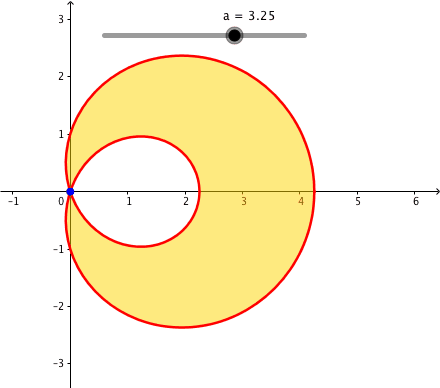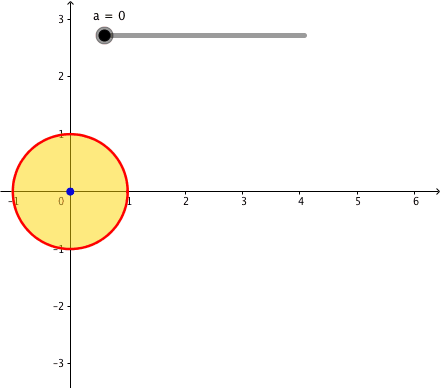
Abb. 1: Pascalsche Schnecken
FŸr den orientierten FlŠcheninhalt A der Pascalschen Schnecke erhalten wir:
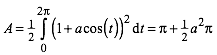(2)
Bei a > 1 wird fŸr die FlŠchenberechnung das Innere der Schleife ausgespart (Abb. 1).
Die Pascalschen Schnecken sind nach ƒtienne Pascal (1588 -1651, Vater von Blaise Pascal) benannt.
3 RegelmŠ§ig verteilte Punkte
Wir
wŠhlen eine natŸrliche Zahl n und
einen Parameterwert t im Intervall 
. Dann definieren wir:
(3)
Auf dem Einheitskreis sind das n regelmŠ§ig verteilte Punkte, die ein regelmŠ§iges n-Eck bilden. Eine VerŠnderung von t bewirkt eine Drehung des regelmŠ§igen n-Eckes.
Nun seien Ek, k = 1 ... n, die Punkte mit den Polarkoordinaten:
(4)
Diese Punkte liegen auf der durch (1) definierten Pascalschen Schnecke. Sie definieren ein (nicht regelmŠ§iges) n-Eck. Wenn wir t verŠndern, bewegen sich die Punkte Ek auf der Pascalschen Schnecke und das n-Eck Šndert seine Form.
Die
Abbildung 2 zeigt die Kinematik fŸr n
= 7 und a = 0.5. Die vom Ursprung
ausgehenden Strecken zu den Punkten Ek schlie§en gleiche Winkel von 
ein, sie bilden also einen regelmŠ§igen FŠcher.
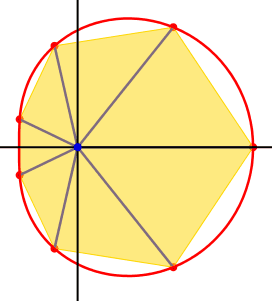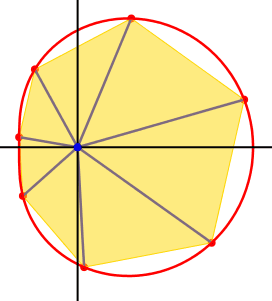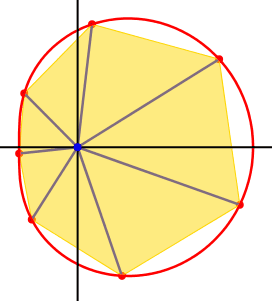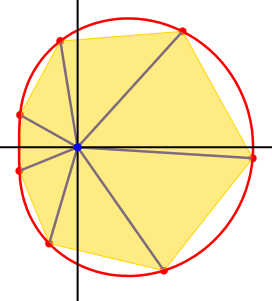
Abb. 2: Einbeschriebenes Vieleck
4 FlŠcheninvarianz
Bei VerŠnderung von t bleibt der orientierte FlŠcheninhalt An des n-Eckes invariant.
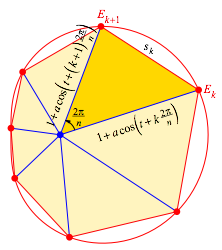
Abb. 3: Beweisfigur
FŸr den Beweis arbeiten wir mit einem Sektordreieck gemŠ§ Abbildung 2. FŸr seinen orientierten FlŠcheninhalt An,k erhalten wir:
(5)
Die orientierte GesamtflŠche An ist daher:
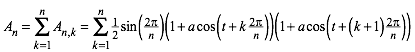(6)
Mit Hilfe der Formeln im Formelapparat (unten) kann An vereinfacht werden zu:
(7)
Da in (7) der Drehparameter t nicht vorkommt, ist An bei einer €nderung von t invariant. Dies war zu zeigen.
Die Abbildung 4 zeigt als weiteres Beispiel die Kinematik fŸr n = 7 und a = 2.
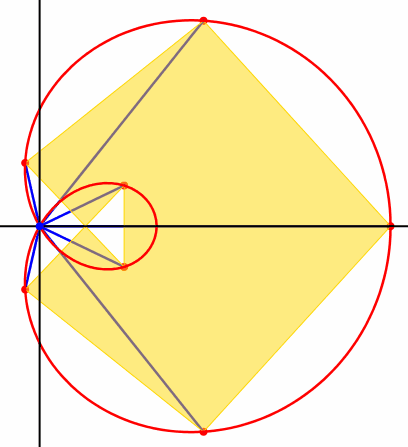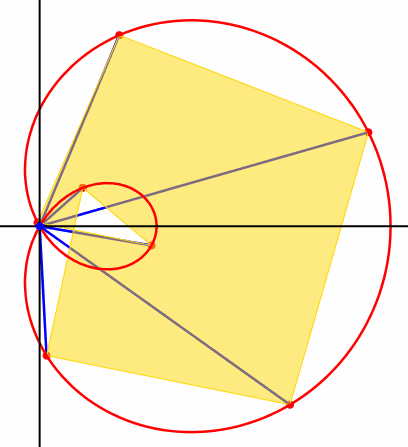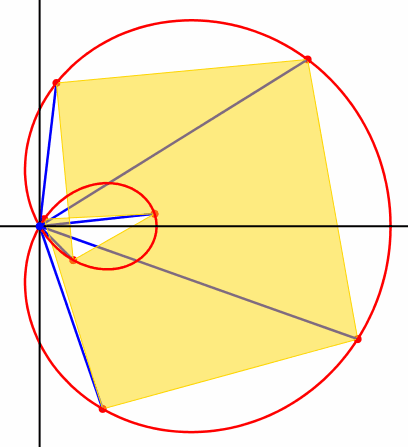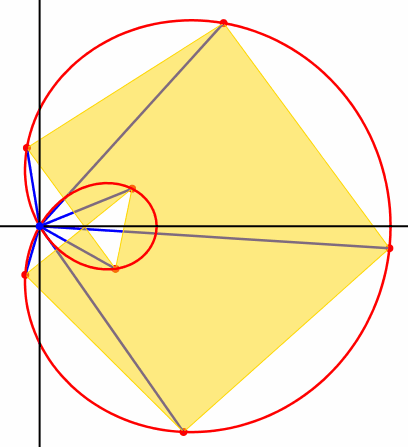
Abb. 4: Invarianter orientierter FlŠcheninhalt
Bei
diesem Beispiel haben wir ein ãŸberschlagenesÒ n-Eck. Die Formel (7) gilt aber auch hier, da wir es bei (5) an der
FŠcherwurzel mit einem orientierten Winkel 
zu tun
haben.
Die Abbildung 5 zeigt den Fall fŸr n = 25 und a = 4.
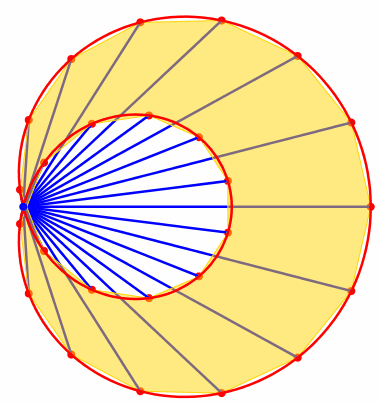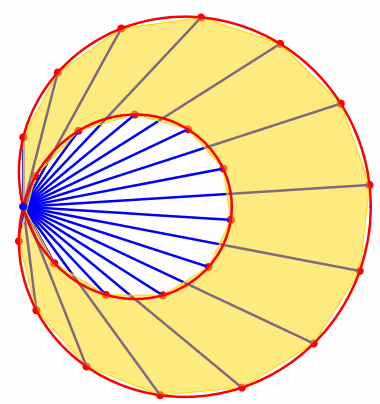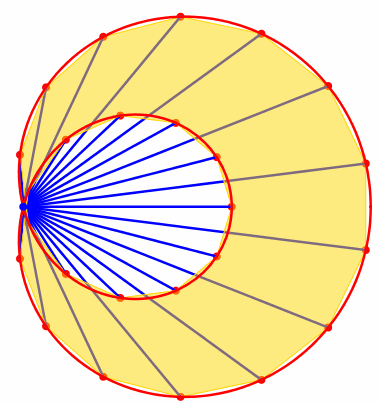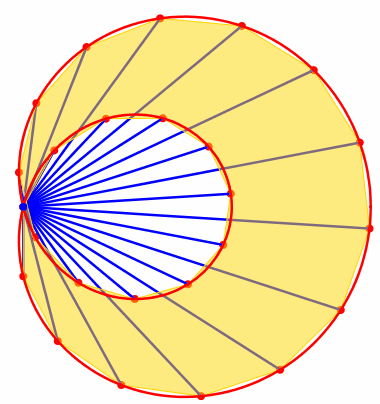
Abb. 5: Approximation der SchneckenflŠche
Aus (7) erhalten wir den Grenzwert:
(8)
Dies stimmt mit (2) Ÿberein.
5 Ein Sonderfall
FŸr n = 4 erhalten wir aus (7):
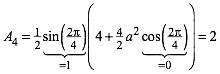(9)
Der orientierte FlŠcheninhalt A4 ist unabhŠngig von a. Wir haben eine Invariante gegenŸber a.
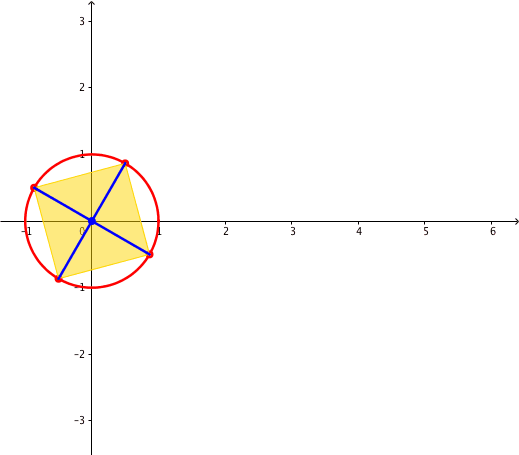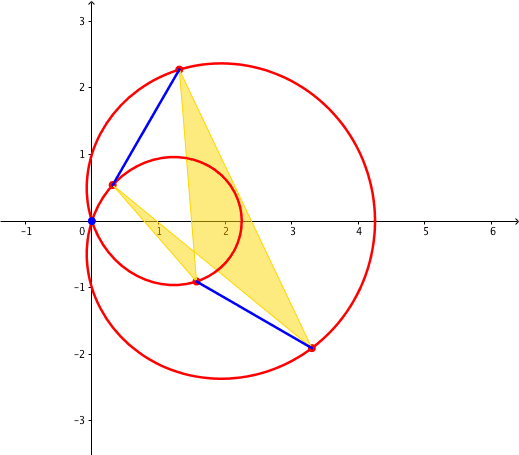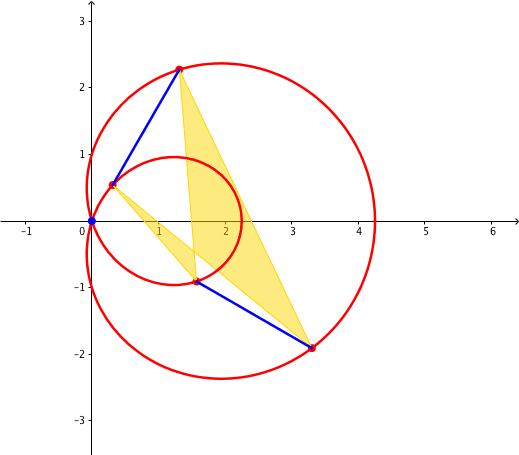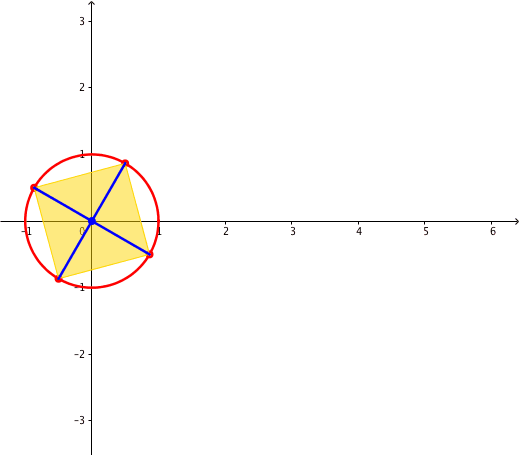
Abb. 6: Invarianter orientierter FlŠcheninhalt
6 Invariante QuadratflŠchensumme
Wir setzen den Seiten sk des n-Eckes Quadrate an (Abb. 7 fŸr n = 7 und a = 0.5).
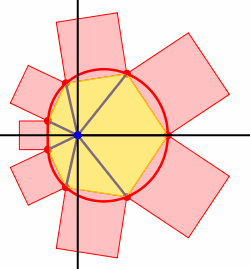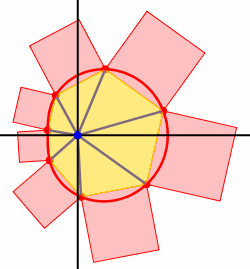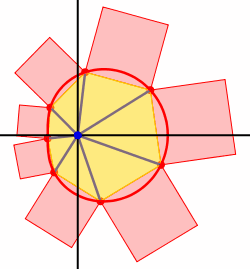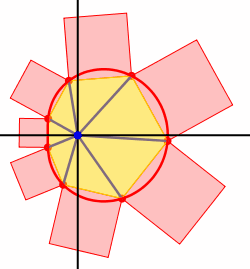
Abb. 7: Quadrate ansetzen
Bei VerŠnderung von t bleibt die Summe der QuadratflŠchen invariant.
Beweis: FŸr das Quadrat der SeitenlŠnge sk (Abb. 3) erhalten wir mit dem Kosinussatz:
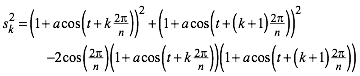(10)
Daraus ergibt sich mit den Formeln aus dem Formelapparat:
(11)
Diese Summe ist unabhŠngig von t.
Die Abbildung 8 zeigt die Situation fŸr n = 7 und a = 2.
Abb. 8
Die Abbildung 9 zeigt die Situation fŸr n = 25 und a = 4.
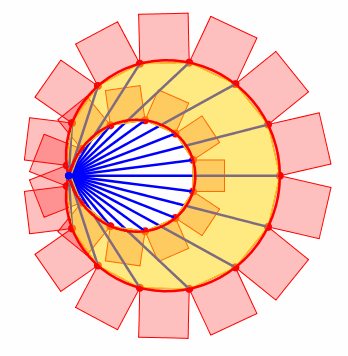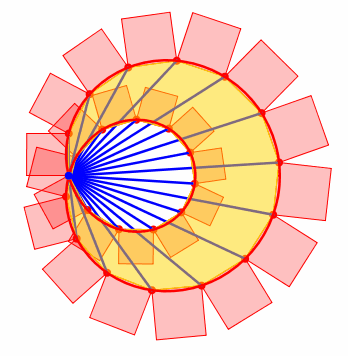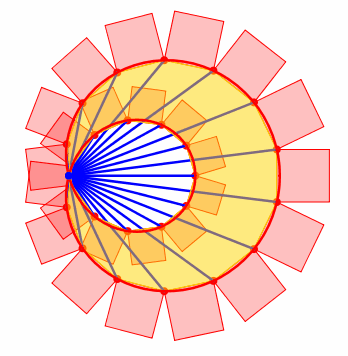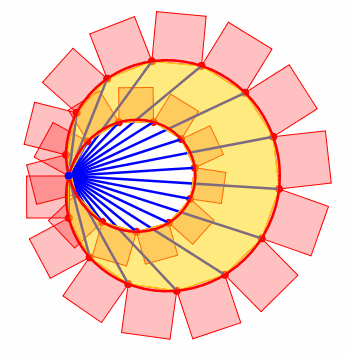
Abb. 9
7 Formelapparat
Beweise fŸr die nachfolgenden Formeln
7.1 Summe und Differenz von Winkeln
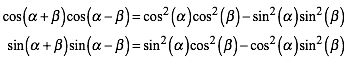(12)
7.2 Zyklische Summen
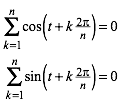(13)
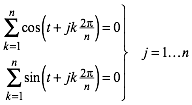(14)
7.3 Zyklische Summen mit Quadraten
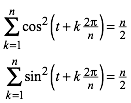(15)
7.4 Zyklische Summe eines Produktes
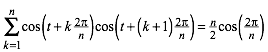(16)
Websites
Hans
Walser: Kardioide und invariante FlŠchen
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide9/Kardioide9.htm