Hans Walser, [20110129a]
Pentagramma mirificum
Anregung: [Heinrich
2010]
1 Worum es geht
Ein Pentagramma
mirificum ist ein sphŠrisches Pentagramm mit rechten Winkeln an den Spitzen.
Die Abbildung zeigt ein Beispiel in stereografischer Projektion. Der blaue Kreis
ist der Hauptkreis (Bild des €quators in Standarddisposition).
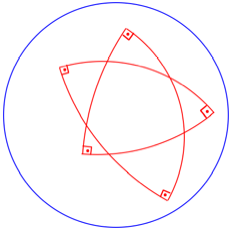
Pentagramma mirificum
1.1
Pol und Polare
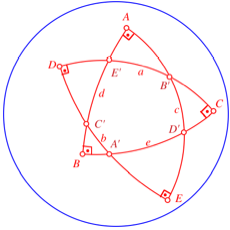
Bezeichnungen
Wegen der rechten
Winkel bei C und D ist 
ein Pol zu a. Daher haben die Bšgen 
, 
, 
und 
alle die LŠnge 
. Analog fŸr die Ÿbrigen vier Seiten des Pentagramms.
1.2
Konstruktion
Wir beginnen mit einem
bei A rechtwinkligen Dreieck 
.
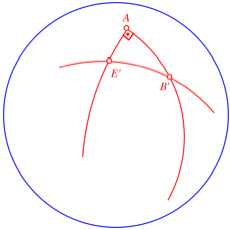
Erster Schritt
Nun zeichnen wir 
. Der Schnittpunkt mit dem Gro§kreis 
sei D, der Schnittpunkt mit dem Gro§kreis 
sei 
und der
Schnittpunkt mit dem Gro§kreis 
sei E. Es ergeben sich die beiden rechten Winkel bei D und E.
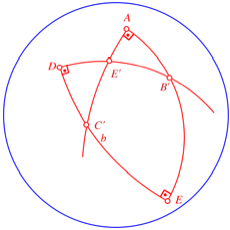
Zweiter Schritt
Als letztes zeichnen
wir 
. Wir erhalten die Schnittpunkte und rechten Winkel gemŠ§
Abbildung. Damit ist das Pentagramma mirificum komplett.
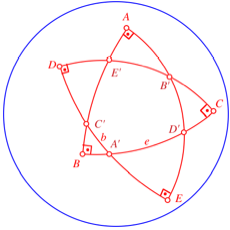
Dritter und letzter
Schritt
Als Folge der rechten
Winkel sind 
der Gro§kreis 
, 
der Gro§kreis 
und 
der Gro§kreis 
.
Wir haben eine
erstaunliche fŸnfteilige Schlie§ungsfigur.
In der folgenden
Abbildung sind auch noch das Pentagramm 
eingezeichnet.
Dieses Pentagramm hat die SeitenlŠnge 
.
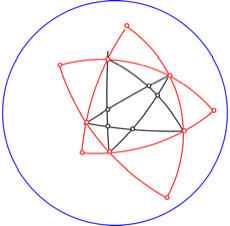
Kleines Pentagramm
2
Das regelmŠ§ige Pentagramma mirificum
2.1
Berechnungen
Die Abbildung zeigt das
regelmŠ§ige Pentagramma mirificum.
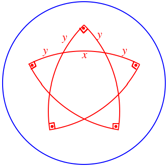
RegelmŠ§iges Pentagramma
mirificum
FŸr die eingezeichneten
BogenlŠngen x und y gilt zunŠchst:
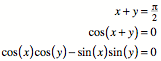
Der sphŠrische
Pythagoras liefert 
. Damit erhalten wir:
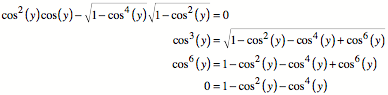
Damit wird:
Uns interessiert nur
die reelle Lšsung, also 
. Hier erscheint der goldene Schnitt (vgl. [Walser 2009]).
2.2
Der goldene Schnitt
Mit der Bezeichnung 
erhalten wir:
Wegen 
folgt:
2.3
Diagonalen
Wir fŸhren nun auch
noch die inneren Diagonalen ein.
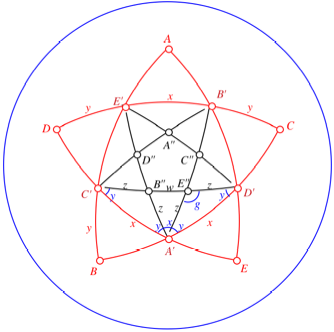
Diagonalen und
Bezeichnungen
Auf Grund der
PolaritŠtsbeziehungen erscheinen x und y nun auch als Winkel. Diese sind in der Abbildung
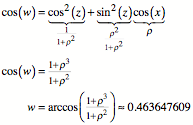
blau markiert. Wir berechnen z und
w. Der Sinn dieser fŸrchterlichen
Rechungen ist, nachher ein handfestes Modell zu bauen.
Im Dreieck 
erhalten wir mit
dem Winkel-Kosinus-Satz:
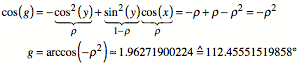
Mit dem
Seiten-Kosinus-Satz ergibt sich weiter:
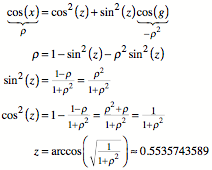
Im Dreieck 
ergibt sich mit
dem Seiten-Kosinus-Satz:
2.4
Streifenmodell
FŸr ein Streifenmodell
(vgl. [Walser 2010]) brauchen wir Streifen nach folgendem Ma§muster. Dabei ist 
, 
, 
und 
.
Vom ersten Streifentyp
(rot) benštigen wir 5 Exemplare, diese Streifen beranden das regelmŠ§ige
Pentagramma mirificum. Vom zweiten Streifentyp (schwarz) benštigen wir ebenfalls
5 Exemplare, diese Streifen bilden die Diagonalen. Der dritte Streifen (blau)
kann optional fŸr den Hauptkreis (€quator) verwendet werden, wir benštigen nur
ein Exemplar.
Wir erhalten damit je
ein regelmŠ§iges Pentagramma mirificum auf jeder HalbsphŠre. Wenn wir nur eine
HalbsphŠre mit einem regelmŠ§igen Pentagramma mirificum haben wollen, brauchen
wir von den roten und schwarzen Streifen nur je die HŠlfte.
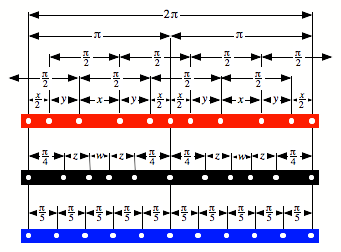
Streifenmuster
Die folgende Abbildung
zeigt die obere HalbsphŠre in stereografischer Projektion.
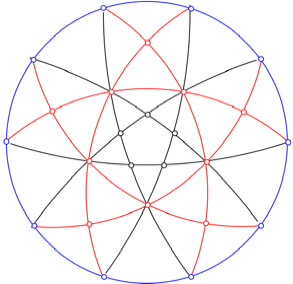
Ober HalbsphŠre
Die folgenden
Abbildungen zeigen ein Halbkugelmodell. Das Penatgramma mirificum wird durch
gelbe Streifen gebildet. Die Diagonalen sind schwarz und der €quator grŸn.
Zuerst ein SchrŠgbild und dann ein Bild von ganz oben.
Halbkugelmodell
Instruktiv ist auch ein
Blick ins Innere der Halbkugel.
Sicht von innen
Literatur
[Heinrich 2010] Heinrich, Frank: Pentagrammafigurationen. MU Der Mathematikunterricht. Elemente nichteuklidischer Geometrien. Jahrgang 56. Heft 6. Dezember 2010. Friedrich Verlag, Seelze. S. 39-52.
[Walser 2009] Walser, Hans: Der Goldene Schnitt. 5., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig 2009. ISBN 978-3-937219-98-1
[Walser 2010] Walser, Hans: Handgreifliche Modelle der Kugelgeometrie und der hyperbolischen Geometrie. MU Der Mathematikunterricht. Elemente nichteuklidischer Geometrien. Jahrgang 56. Heft 6. Dezember 2010. Friedrich Verlag, Seelze. S. 28-37.