1 Worum geht es?

Gelenkmechanismus für den Satz des Pythagoras.

2 Perigal-Zerlegungsbeweis des Satzes von Pythagoras

Die Abbildung 1 zeigt den klassischen Zerlegungsbeweis für den Satz von Pythagoras nach Perigal (Henry Perigal, 1801-1898).

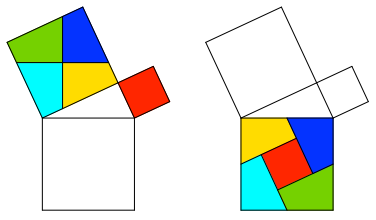
Abb. 1: Zerlegungsbeweis nach Perigal

3 Formaler Beweis

Die Abbildung 1 ist natürlich kein Beweis. Es muss noch gezeigt werden, dass die Teilfiguren links kongruent zu den entsprechenden Teilfiguren rechts sind.

Dazu arbeiten wir mit den Bezeichnungen der Abbildung 2.

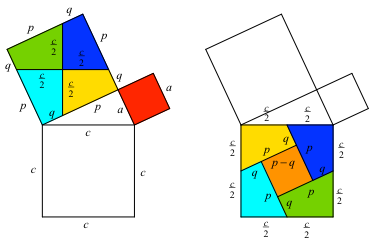
Abb. 2: Bezeichnungen

Das orange Quadrat rechts hat zunächst die Seitenlänge p – q. Es ist zu zeigen, dass diese Seitenlänge gleich a ist.

Durch Einzeichnen einer Parallelen zur Hypotenuse (Abb. 3, links) können wir mit einer Parallelogramm-Überlegung zeigen, dass dies tatsächlich der Fall ist.

Abb. 3: Beweisfigur

4 Farbanordnungen

Im großen Kathetenquadrat und im Hypotenusenquadrat sind die zyklischen Reihenfolgen der Teile gold, blau, grün und hellblau ungleich.

Die Teile gold und grün gehen durch eine Translation ineinander über, die Teile blau und hellblau durch eine Punktspiegelung. Diese Unterschiede sind durch den nachfolgend gezeigten Gelenkmechanismus bedingt.

An sich, also ohne Bezugnahme auf den Gelenkmechanismus, könnten diese Unterschiede durch die Vertauschung der Farben blau und hellblau in einer der beiden Figuren der Abbildung 1 behoben werden.

5 Die Gelenkkette

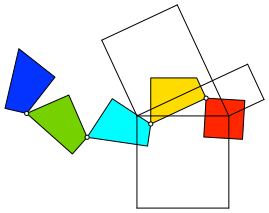
Abb. 4: Gelenkkette

Die Abbildung 4 zeigt die Gelenkkette. Die fünf Teile sind durch vier Gelenke verbunden.

6 Gelenkbeweis

Die Abbildung 5 zeigt den Gelenkbeweis.

Abb. 5: Gelenkbeweis

Weblinks

Hans Walser: Aufwickel-Pythagoras

http://www.walser-h-m.ch/hans/Miniaturen/A/Aufwickel-Pythagoras3/Aufwickel-Pythagoras3.htm

Hans Walser: Aufwickel-Pythagoras

http://www.walser-h-m.ch/hans/Miniaturen/A/Aufwickel-Pythagoras2/Aufwickel-Pythagoras2.htm

Hans Walser: Aufwickel-Pythagoras

http://www.walser-h-m.ch/hans/Miniaturen/A/Aufwickel-Pythagoras/Aufwickel-Pythagoras.htm

Hans Walser: Perigal

http://www.walser-h-m.ch/hans/Miniaturen/P/Perigal/Perigal.html