Hans Walser, [20071205b]
Perlenkette
1 Problemstellung
Auf einer durch eine beliebige parametrisierten Kurve (im Raum oder in der Ebene) soll in jeweils gleichen AbstŠnden ein Punkt markiert werden.
Die Kurve mźsste also in so genannten natźrlichen Parameter (KurvenlŠnge als Parameter) umgeschrieben werden. Zur Berechnung der KurvenlŠnge braucht es ein Integral, das nicht immer geschlossen lšsbar ist.
Ich bearbeite die Sache daher diskretisiert und rein numerisch, orientiere mich aber an den Formeln der Differentialgeometrie.
2 Programm
MuPAD-Programm
fźr die Kosinuskurve. Dabei zŠhlt N
die Anzahl der Intervalle zwischen den Perlen. Der Parameterbereich ist ![]() .
.
x:=t->t:
y:=t->cos(t):
N:=10:
a:=-PI:
b:=PI:
dt:=0.001:
K:=ceil((b-a)/dt):
dx:=t->(x(t+dt)-x(t))/dt:
dy:=t->(y(t+dt)-y(t))/dt:
dxBetrag:=t->sqrt(dx(t)^2+dy(t)^2):
s[0]:=0:
for k from 1 to K do
s[k]:=s[k-1]+dxBetrag(a+(k-1)*dt)*dt:
end_for:
print(Unquoted,
"Bogenlaenge = ".float( s[K])):
deltas:=s[K]/N:
j[0]:=0:
for n from 1 to N do
k:=j[n-1]:
while s[k]/deltas<n or s[k]/deltas=n
do
k:=k+1:
end_while:
j[n]:=k:
end_for:
j[N+1]:=K:
Kurve:=plot::Curve2d([x(t),
y(t)], t=a..b, LineColor=[0,0,1]):
Punkt:=t->plot::Point2d([x(t),
y(t)], PointSize=5, PointColor=[1,0,0]):
plot(Kurve,
Punkt(a+j[n]*dt)$n=0..N+1, Scaling=Constrained,
AxesTitleFont=["Times",
12, Italic],TicksDistance=1, TicksBetween=0,
Width=92.4, Height=51.5, BorderWidth=1/4);
Wir erhalten
Bogenlaenge = 7.641210171
und die Figur:
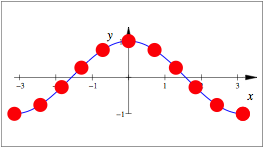
Kosinuskurve als Perlenkette
3 Beispiele
3.1 Kreis
x:=t->cos(t):
y:=t->sin(t):
N:=12:
a:=0:
b:=2*PI:
Das ergibt
Bogenlaenge = 6.283999738
und die Figur:
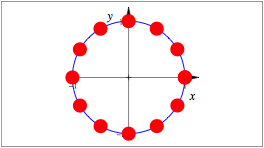
Kreis
3.2 Ellipse
x:=t->2*cos(t):
y:=t->sin(t):
N:=12:
a:=0:
b:=2*PI:
Das ergibt
Bogenlaenge =
9.68926251
und die Figur:
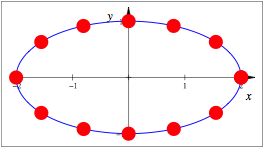
Ellipse
Nun ist zwar die Ellipse ein horizontal affin verzerrter Kreis; die Perlen gehorchen aber nicht dieser Verzerrung. Wir sehen das, wenn wir dem Kreis einen Quadratraster und der Ellipse den entsprechenden Rechtecksraster unterlegen.
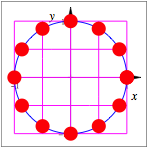
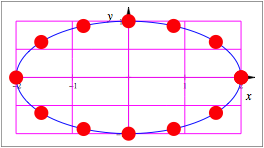
Kreis und Ellipse
3.3 Kettenlinie
Die Kettenlinie ist zwar mathematisch ein ăschlechtesŇ Beispiel, weil sich die LŠnge der Kosinushyperbolikus-Kurve geschlossen berechnen lŠsst. Trotzdem als Beispiel einer ăechtenŇ Kette.

Kettenlinie
3.4 RegelmŠ§iges Fźnfeck
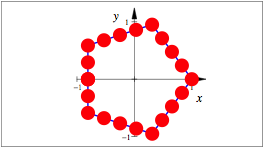
RegelmŠ§iges Fźnfeck
3.5 Archimedische Spirale
r:=t->0.5+0.02*t:
x:=t->r(t)*cos(t):
y:=t->r(t)*sin(t):
N:=500:
a:=0:
b:=20*PI:

Archimedische Spirale