Hans Walser, [20150828], [20161221]
Permutationen
1 Worum geht es?
Wir kšnnen n Elemente auf n! Arten anordnen.
Im Folgenden wird eine Visualisierung mit regelmŠ§igen n-Ecken versucht die jeweils in n Sektoren unterteilt sind. Die Elemente werden durch Farben angegeben.
2 Technisches
Es ist:
![]() (1)
(1)
Die Tabelle 1 gibt die numerischen Werte fźr die FakultŠten an. Sie geben die Anzahl Permutationen von n Elementen.
|
n |
n! |
|
n |
n! |
|
1 |
1 |
|
6 |
720 |
|
2 |
2 |
|
7 |
5040 |
|
3 |
6 |
|
8 |
40320 |
|
4 |
24 |
|
9 |
362880 |
|
5 |
120 |
|
10 |
3628800 |
Tab. 1: FakultŠten
Fźr die Farben wird der Code der Tabelle 2 verwendet. In der Regel wird Schwarz weggelassen.
|
Nr. |
RGB |
Farbe |
Beispiel |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
1,0,0 |
Rot |
|
|
5 |
|
Magenta |
|
|
6 |
1,1,0 |
Gelb |
|
Tab. 2: Farbcode
3 Beispiele
3.1 Eine Farbe
Da es kein Eineck gibt, behelfen wir uns mit einem Tropfen. Eine Farbe kann nur auf eine Art permutiert werden.

Abb. 1: Eine Farbe
3.2 Zwei Farben
Wir behelfen uns mit einer Linse.

Abb. 2: Zwei Farben
3.3 Drei Farben
Wir kšnnen mit einem Dreieck arbeiten. Es gibt 3! = 6 FŠrbungsmšglichkeiten.
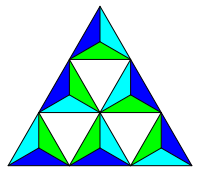
Abb. 3: Drei Farben
3.4 Vier Farben
Unter den 4! = 24 Quadraten sind keine zwei gleich gefŠrbt.

Abb. 4a: Vier Farben

Abb. 4b: Andere Anordnung
3.5 Fźnf Farben
Wir haben 5! = 120 Fźnfecke zu kolorieren. Leider gibt es kein schšnes Raster fźr Fźnfecke, so dass wir etwas improvisieren mźssen.

Abb. 5: Fźnf Farben
3.6 Sechs Farben
Wir haben 6! = 720 Sechsecke, jedes anders gefŠrbt.

Abb. 6: Sechs Farben
Die Abbildung 7 zeigt einen Ausschnitt aus dem Zentrum.

Abb. 7: Ausschnitt