Hans Walser, [20190404]
¹ = 3
Und er machte das Meer, gegossen, von einem Rand zum andern zehn Ellen weit, ganz rund und fŸnf Ellen hoch, und eine Schnur von drei§ig Ellen war das Ma§ ringsherum. 1. Kšnige 7, 23
1 Worum geht es?
Wir gehen davon aus, dass wir die Grš§e von ¹ nicht kennen, hingegen wissen, dass sich der FlŠcheninhalt A des Kreises mit dem Radius r nach der Formel
(1)
berechnet.
Mit einer Anteilberechnung der KreisflŠche im Quadrat kšnnen wir ¹ berechnen.
2 Kreisanteil in Quadrat und Rechteck
Der rote Kreis (Abb. 1) hat den Radius 1, das umbeschriebene Quadrat daher die SeitenlŠnge 2.
Abb. 1: Kreis und Quadrat
FŸr den FlŠchenanteil des roten Kreises an der Gesamtfigur gilt also:
(2)
Das gilt natŸrlich auch fŸr eine Folge von sechs Kreisen im Rechteck (Abb. 2).
Abb. 2: FlŠchenanteil ¹/4
3 Kreisring
Nun biegen wir das Rechteck zum Kreisring auf (Abb. 3).
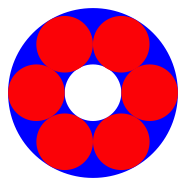
Abb. 3: Kreisring
Diese Figur kennen wir: sechs MŸnzen um eine zentrale MŸnze herumgelegt (Abb. 4).
Abb. 4: MŸnzen
Der Innenradius des Ringes der Abbildung 3 ist also 1, der Au§enradius 3. FŸr den FlŠcheninhalt des Kreisringes erhalten wir:
(3)
Der FlŠchenanteil der sechs roten Kreise am gesamten Ring ist daher:
(4)
Der Vergleich mit (2) ergibt:
(5)
Dies war zu beweisen.
Wo steckt der Fehler?