Hans Walser, [20220417]

Planetenbahn

Idee und Anregung: D. O., V.

1 Worum geht es?

Schrittweise Modellierung der Planetenbahn

2 Disposition

Wir setzen den Zentralkörper („Sonne“) in den Koordinatenursprung.

Der Startpunkt des Planeten („Mars“) sei px[0] := 1: py[0] := 0:, und die Startgeschwindigkeit vx[0] := 0: vy[0] := 75;. Wir variieren in unseren Beispielen lediglich vy[0].

Der Planet befindet sich also im Aphel oder im Perihel.

Die Abbildung 1 zeigt die Situation für v₀ = 0.75.

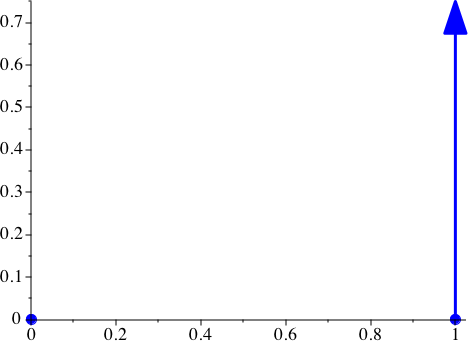
Abb. 1: Disposition. vy[0] = 0.75

3 Gravitation

Die Gravitation wird beschrieben durch: G/r^k.

Dabei ist G eine Konstante und r der Abstand des Planeten vom Zentralkörper. Der Exponent von r wird mit k bezeichnet.

Wie setzen im Folgenden vorerst G = 1. Für die Newtonsche Mechanik ist k = 2.

4 Modelliertechnisches

Schrittlänge dt.

Zu Visualisierungszwecken werden dp Schritte zusammengefasst.

Modellierungsumfang N.

5 Rekursives Vorgehen

5.1 Startwerte:

px[0] := 1: py[0] := 0:

vx[0] := 0: vy[0] := 1;

5.2 Technische Startwerte:

r[0] := sqrt(px[0]^2 + py[0]^2):

P[0] := point([px[0], py[0]], symbol = solidcircle, symbolsize = 15, color = blue):

5.3 Rekursion:

for n from 1 to N+dp do

vx[n] := vx[n-1] - G/r[n-1]^(k+1)*dt*px[n-1]:

vy[n] := vy[n-1] - G/r[n-1]^(k+1)*dt*py[n-1]:

px[n] := px[n-1] + dt*vx[n]:

py[n] := py[n-1] + dt*vy[n]:

r[n] := sqrt(px[n]^2 + py[n]^2):

P[n]:= point([px[n] , py[n] ], symbol = solidcircle, symbolsize = 15, color = blue):

Dreieck[n] := polygon([[0,0], [px[n] , py[n] ], [px[n-1] , py[n-1] ]], color = COLOR(RGB, 1,1- modp(floor((n-1)/dp), 2), 0), style = polygon):

end:

6 Zeichentechnisches

Punkte := seq(P[dp*n], n = 0 .. N/dp):

Kurve := curve([seq([px[n] , py[n] ], n = 0 .. N)], thickness = 2, color = blue):

Dreiecke := seq(Dreieck[n], n= 1 .. N):

Zentralkoerper := point([0 ,0 ], symbol = solidcircle, symbolsize = 15, color = blue):

v0 := arrow([1,0], [1+vx[0], 0+vy[0]], 0, 0.05, 0.1, color = blue, border = [color = blue, thickness = 3]):

display([Kurve , v0, Dreiecke, Zentralkoerper, Punkte]);

7 Sektorenflächen

for n from 0 to N do

Dreiecksflaeche[n] := 1/2*(px[n]*py[n+1] - px[n+1]*py[n]):

end:

for m from 0 to floor(N/dp-1) do

Summe[m] := sum(Dreiecksflaeche[j],j = m*dp .. (m+1)*dp ):

print(m+1, Summe[m]):

end:

8 Illustrationsbeispiele

In der Abbildung 2 ist lediglich die Bahnkurve gezeichnet. Sie ist ein Polygonzug. Die in Schritten von dt gezeichneten Punkte sind geradlinig verbunden. Da dt sehr klein ist, sehen wir eine gekrümmte Kurve. Die Bahnkurve ist eine Ellipse mit dem Zentralkörper in einem der beiden Brennpunkte.

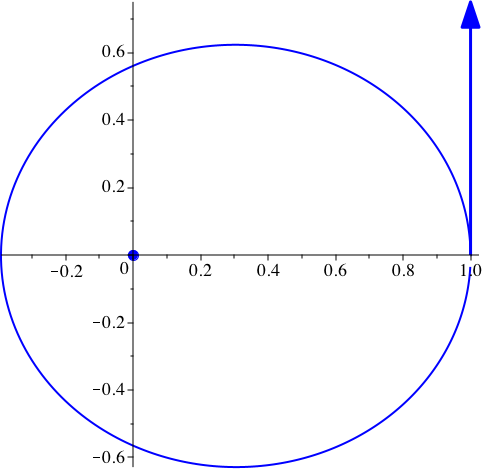
Abb. 2: Bahnkurve. vy[0] = 0.75, G = 1, k = 2, dt = 0.01, N = 360

In der Abbildung 3 ist in jedem gerechneten Punkt der Planet eingezeichnet. Gibt eine dicke Kurve.

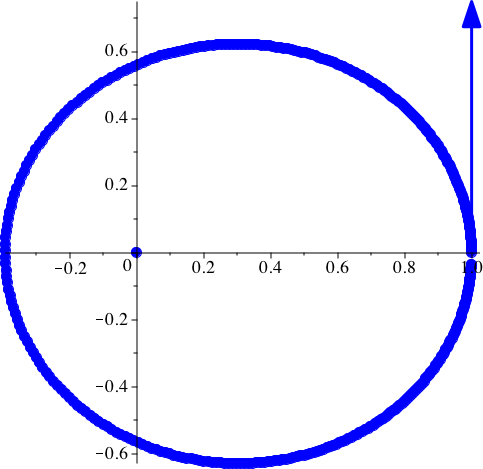
Abb. 3: Positionen des Planeten. vy[0] = 0.75, G = 1, k = 2, dt = 0.01, dp = 1, N = 360

In der Abbildung 4 ist nur bei jedem fünfzehnten Punkt (dp = 15) der Planet eingezeichnet. Dadurch wird die Geschwindigkeit des Planetenumlaufs sichtbar. Bei großer Entfernung vom Zentralkörper ist die Geschwindigkeit klein, in der Nähe des Zentralkörpers dagegen groß.

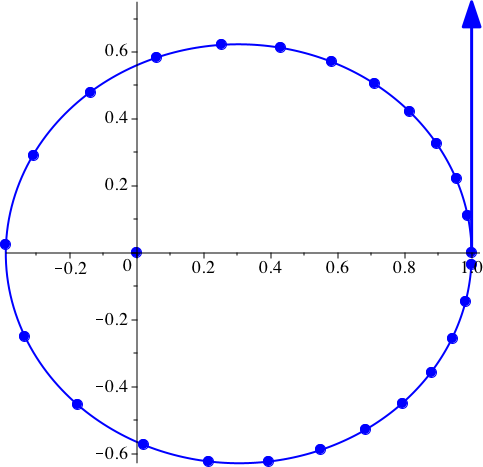
Abb. 4: Ausgedünnte Darstellung. vy[0] = 0.75, G = 1, k = 2, dt = 0.01, dp = 15, N = 360

In der Abbildung 5 sind zusätzlich Sektoren eingezeichnet.

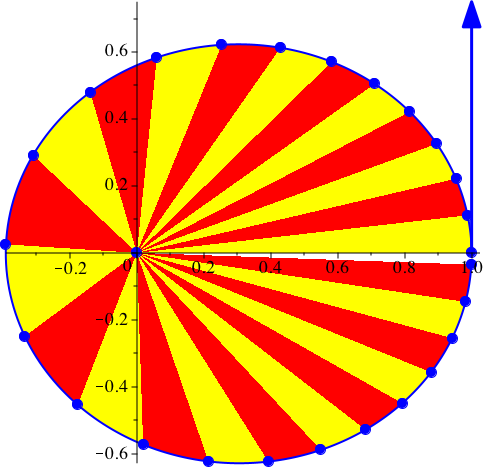
Abb. 5: Sektoren. vy[0] = 0.75, G = 1, k = 2, dt = 0.01, dp = 15, N = 360

In der Abbildung 6 schließlich sind die Planetenpositionen nicht mehr eingezeichnet. Die Sektoren illustrieren das zweite Keplersche Gesetz: Ein vom Zentralkörper zum Planeten gezogener Fahrstrahl überstreicht in gleichen Zeiten gleich große Sektorflächen.

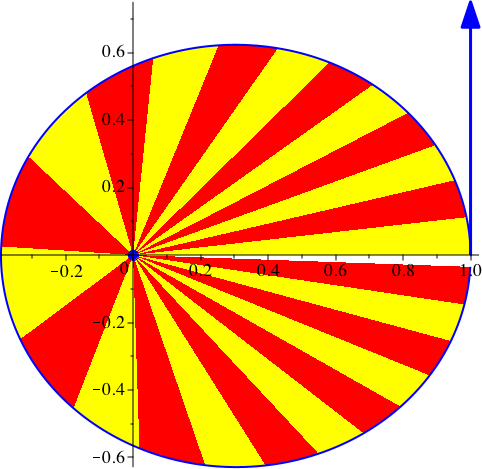
Abb. 6: Nur Sektoren. vy[0] = 0.75, G = 1, k = 2, dt = 0.01, dp = 15, N = 360

Die Tabelle 1 gibt die einzelnen Sektorflächen. Sie sind (praktisch) konstant. Die Streuungen sind technisch bedingt.

Sektornummer	Sektorfläche
1	0.06000000002
2	0.05999999995
3	0.0600000000
4	0.0600000001
5	0.0600000002
6	0.0600000000
7	0.0599999999
8	0.05999999985
9	0.05999999992
10	0.05999999997
11	0.05999999991
12	0.05999999999
13	0.06000000006
14	0.05999999999
15	0.06000000003
16	0.05999999998
17	0.06000000015
18	0.0600000000
19	0.0599999999
20	0.0600000000
21	0.0600000001
22	0.0600000000
23	0.05999999985
24	0.05999999992

Tab. 1: Sektorflächen

Die Abbildung 7 zeigt die Situation animiert.

Abb. 7: Animation. vy[0] = 0.75, G = 1, k = 2, dt = 0.01, dp = 15, N = 360

In der Animation der Abbildung 8 ist zusätzlich der jeweilige Geschwindigkeitsvektor eingezeichnet.

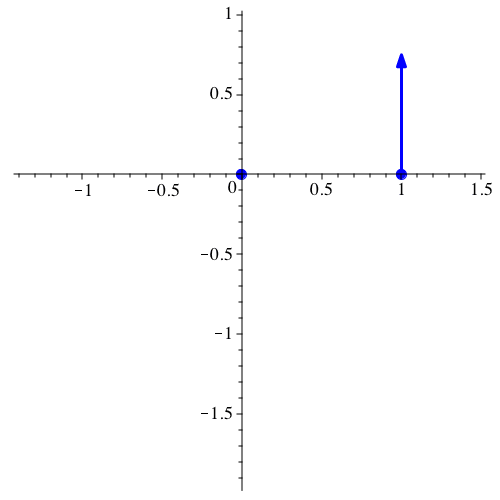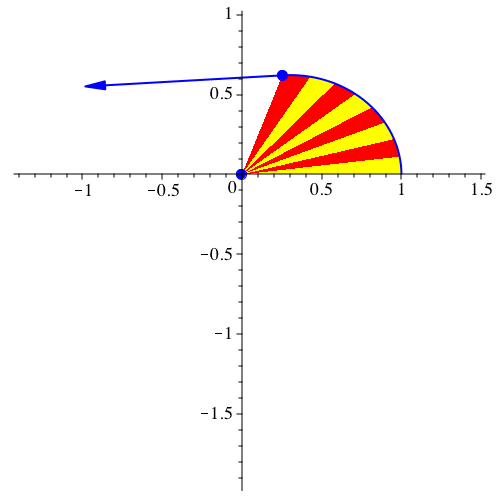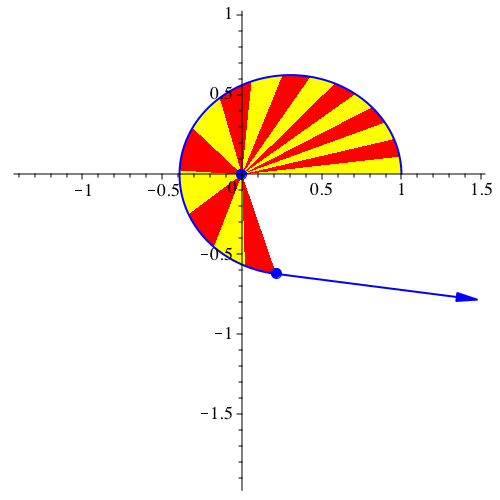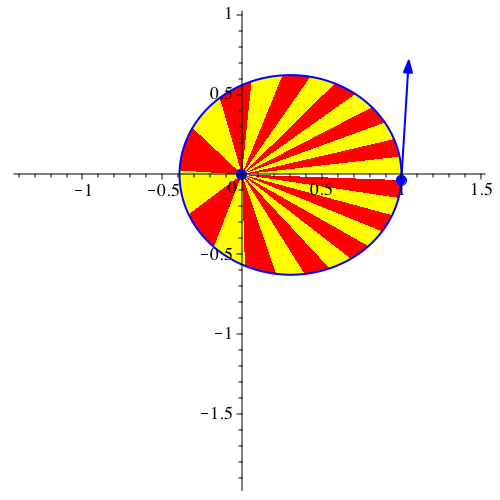
Abb. 8: Geschwindigkeitsvektor

Wir tragen die Geschwindigkeitsvektoren alle vom Ursprung aus ab. So entsteht ein Geschwindigkeitsdiagramm (Abb. 9). Das Geschwindigkeitsdiagramm scheint in diesem Beispiel ein Kreis zu sein.

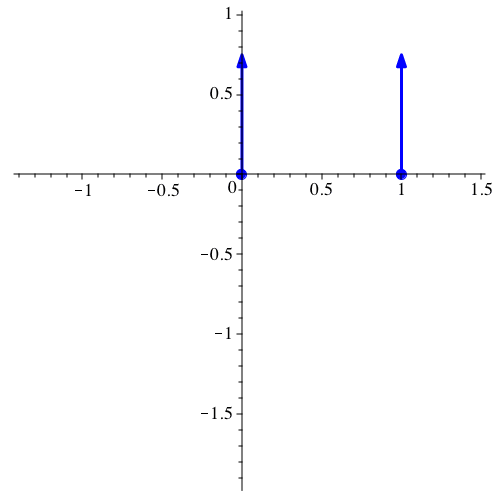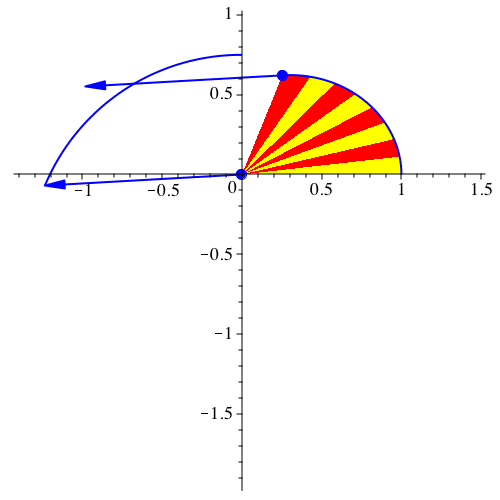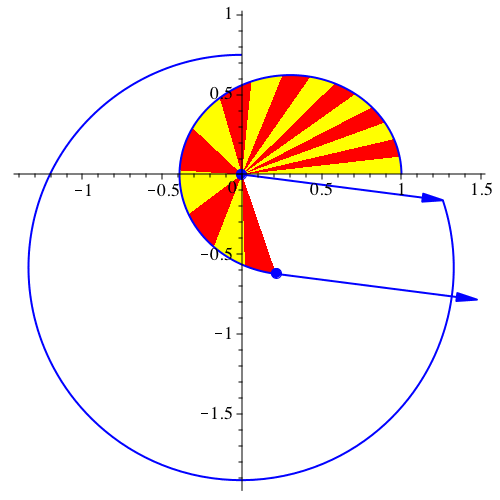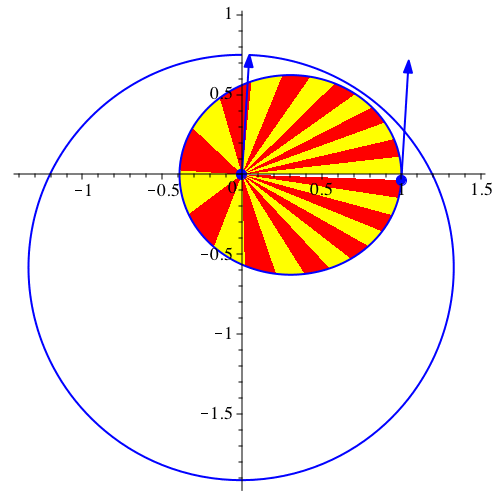
Abb. 9: Geschwindigkeitsdiagramm ein Kreis?

9 Kegelschnitte

Für k := 2 sind die Planetenbahnen Kegelschnitte mit dem Zentralkörper in einem Brennpunkt. Die Kegelschnitte sind zur Kontrolle als Kurven mit Parameterdarstellung grün eingezeichnet. Bei den Beispielen zu Ellipse und Hyperbel ist im Standbild jeweils auch der zweite Brennpunkt eingezeichnet.

Ich vermute, dass das Geschwindigkeitsdiagramm jeweils ein Kreis ist.

9.1 Ellipsen

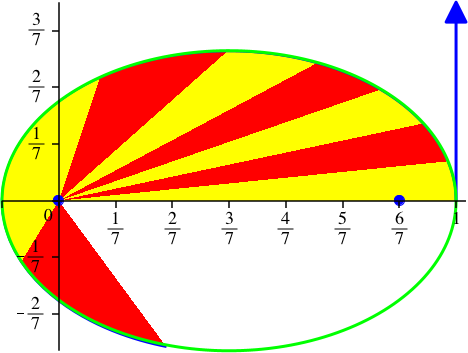
Abb. 10: Ellipse. vy[0] = 1/2, G = 1, k = 2, dt = 0.01, dp = 20, N = 160

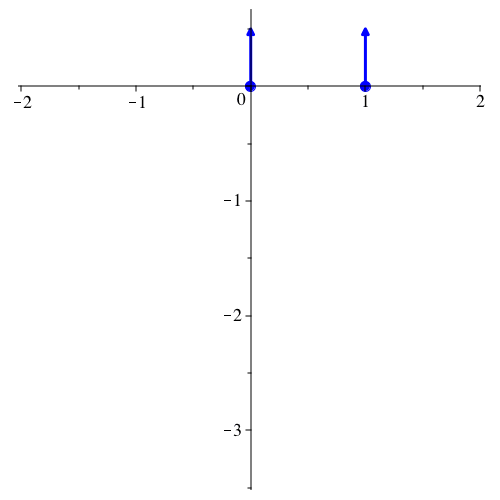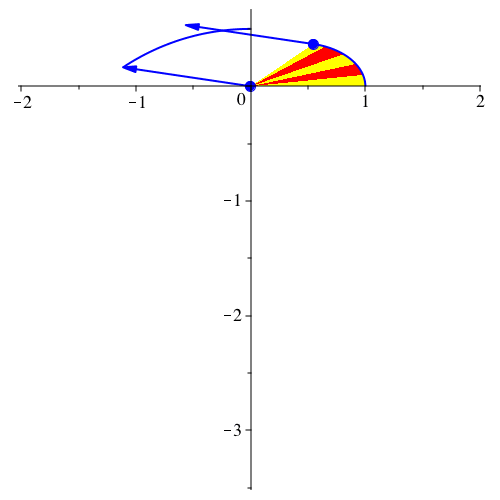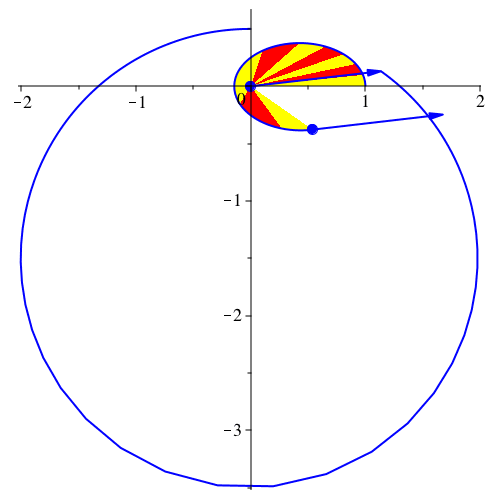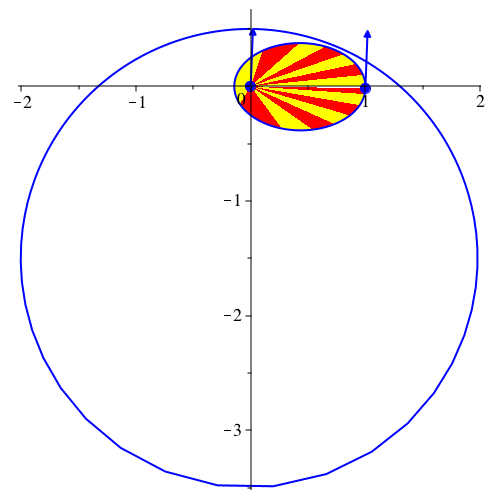
Abb. 11: Ellipse und Geschwindigkeitsdiagramm. vy[0] = 1/2, G = 1, k = 2, dt = 0.01, dp = 20, N = 270

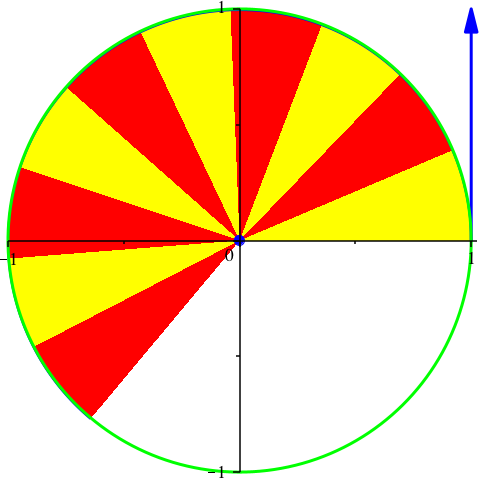
Abb. 12: Sonderfall Kreis. vy[0] = 1, G = 1, k = 2, dt = 0.01, dp = 40, N = 400

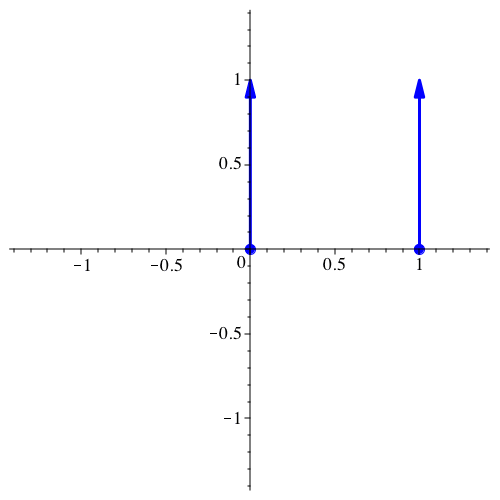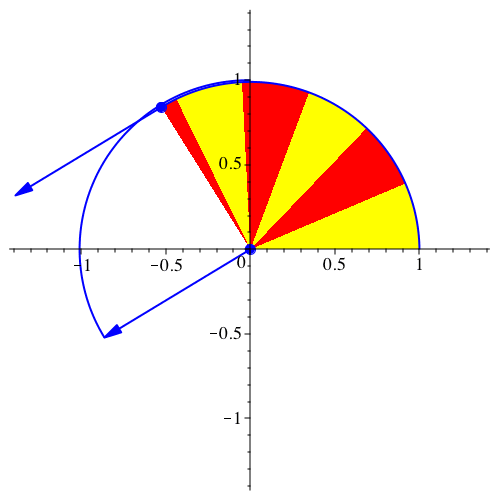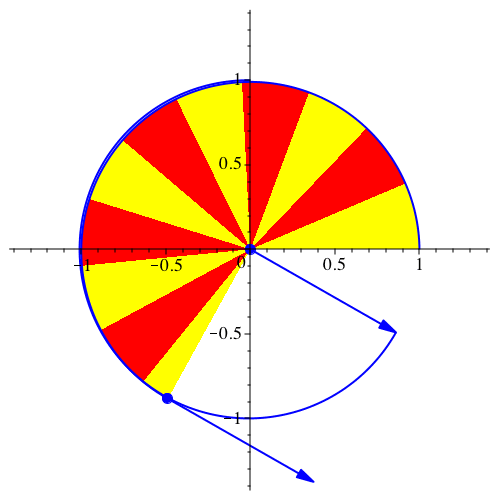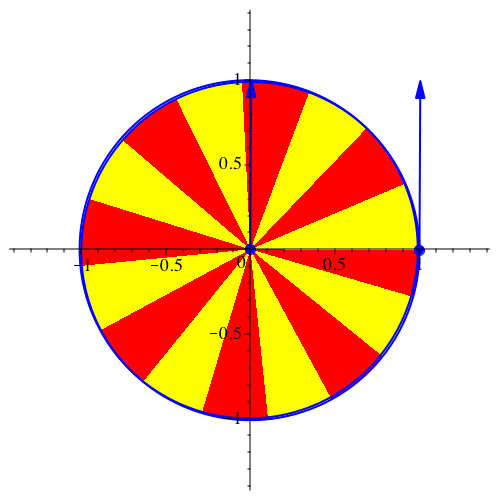
Abb. 13: Sonderfall Kreis. vy[0] = 1, G = 1, k = 2, dt = 0.02, dp = 20, N = 314

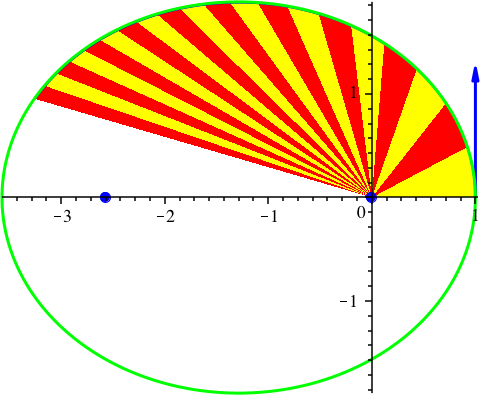
Abb. 14: Nochmals Ellipse. vy[0] = 5/4, G = 1, k = 2, dt = 0.005, dp = 80, N = 1600

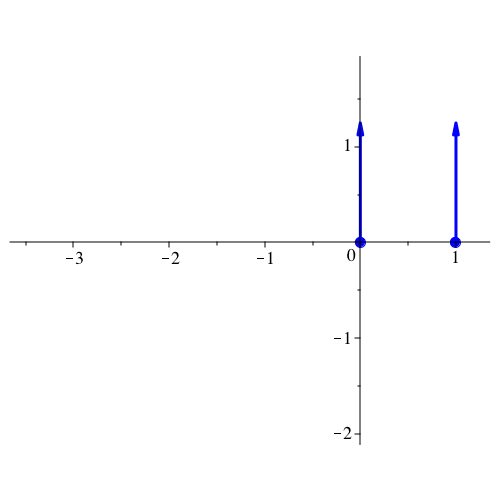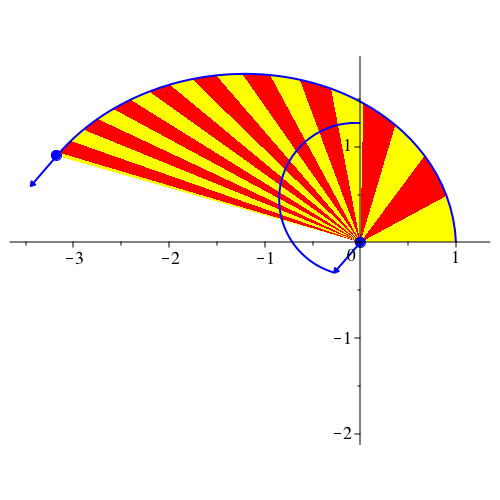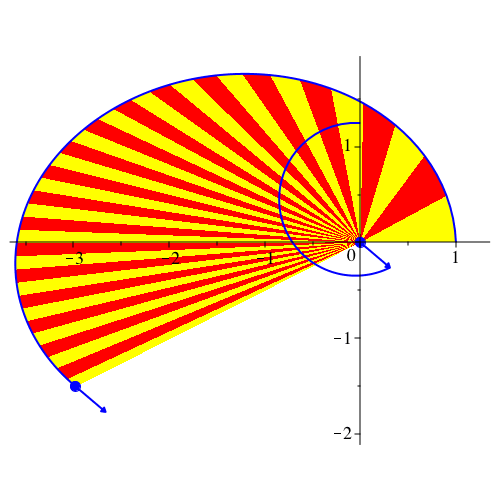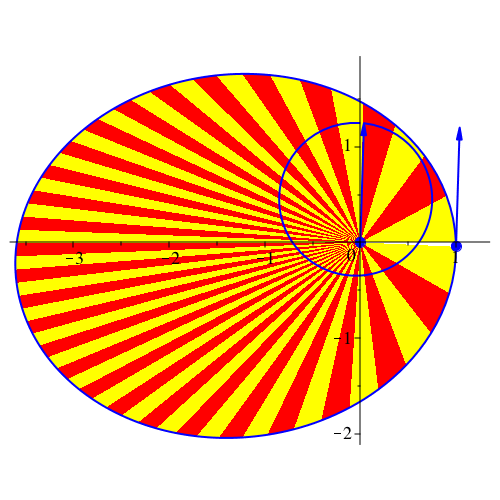
Abb. 15: Nochmals Ellipse. vy[0] = 5/4, G = 1, k = 2, dt = 0.1, dp = 4, N = 220

9.2 Parabel

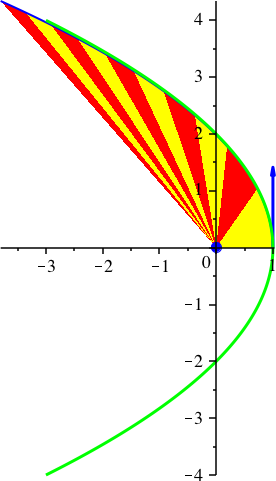
Abb. 16: Parabel. vy[0] = sqrt(2), G = 1, k = 2, dt = 0.01, dp = 80, N = 800

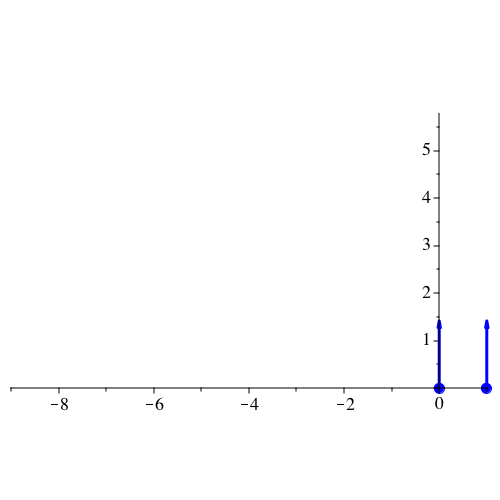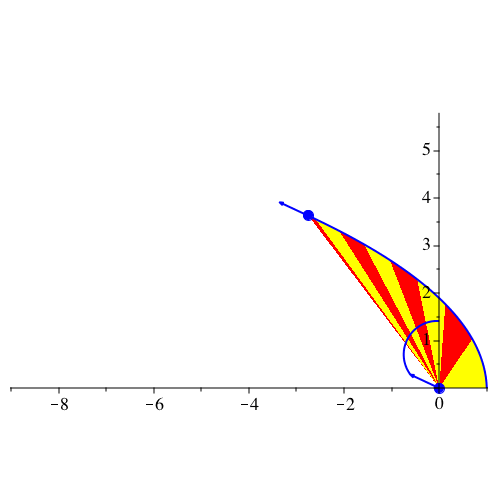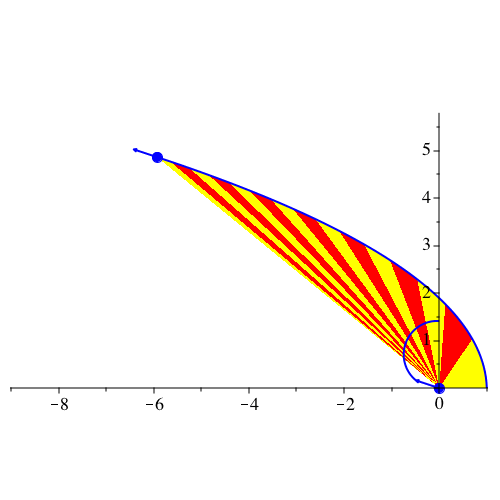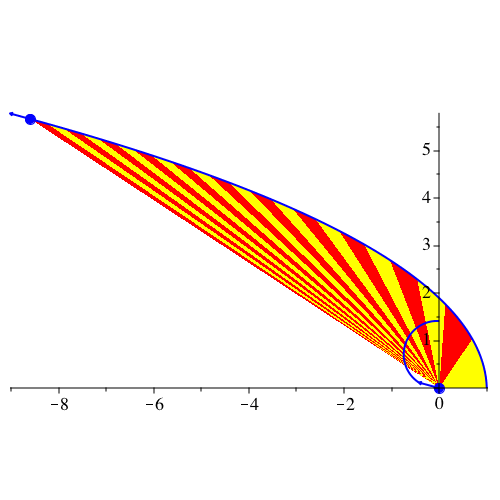
Abb. 17: Parabel. vy[0] = sqrt(2), G = 1, k = 2, dt = 0.08, dp = 10, N = 220

9.3 Hyperbel

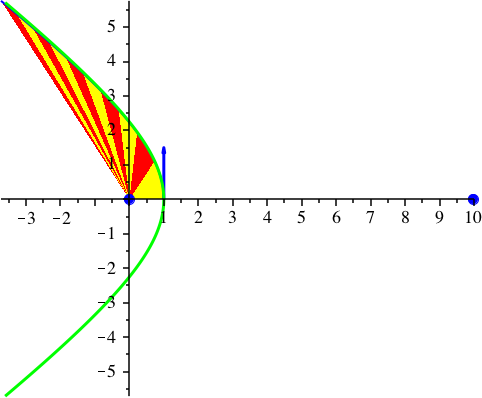
Abb. 18: Hyperbel. vy[0] = 3/2, G = 1, k = 2, dt = 0.01, dp = 80, N = 800

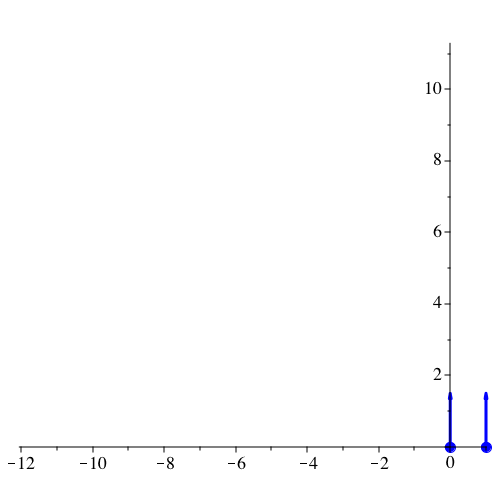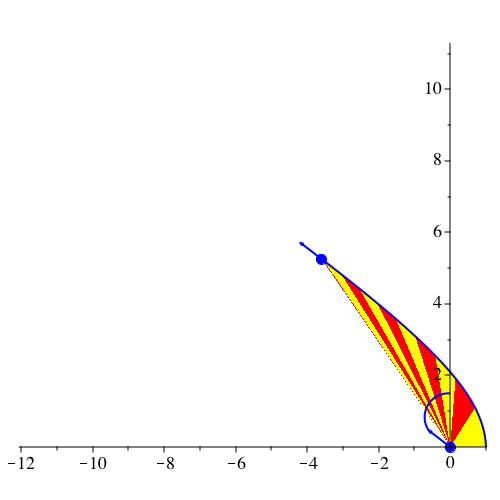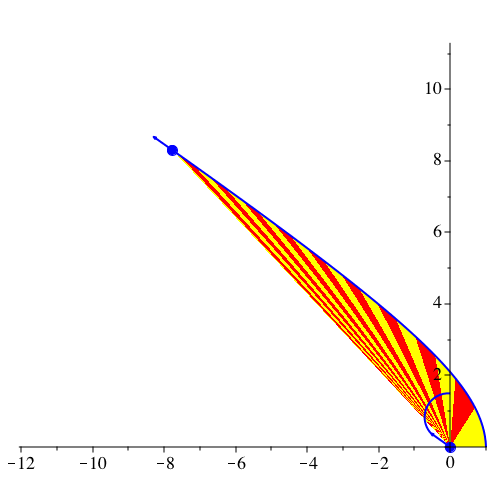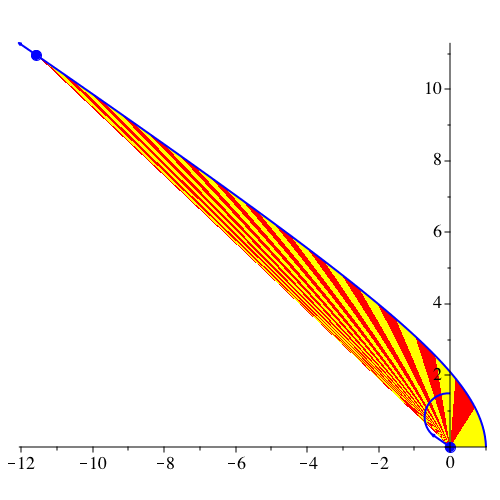
Abb. 19: Hyperbel. vy[0] = 3/2, G = 1, k = 2, dt = 0.1, dp = 8, N = 220

10 Abstoßung

Für negatives G ergibt sich eine Abstoßung (Abb. 20).

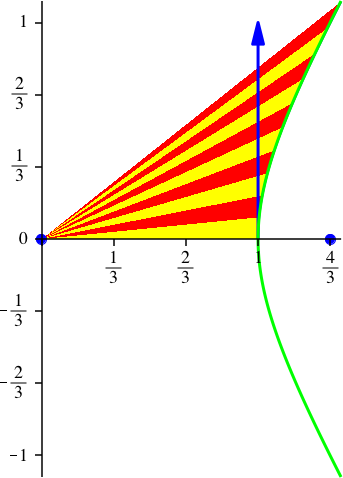
Abb. 20: Abgewandte Hyperbel. vy[0] = 1, G = –1, k = 2, dt = 0.005, dp = 20, N = 200

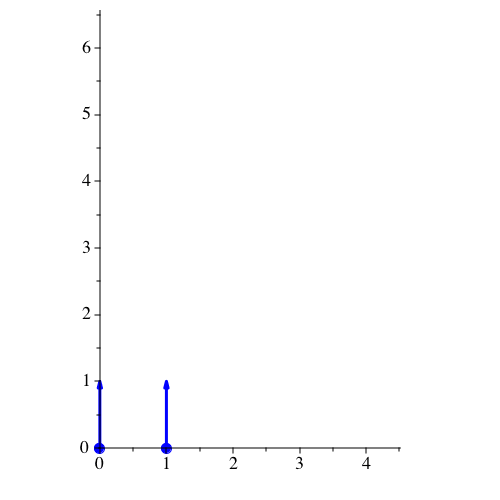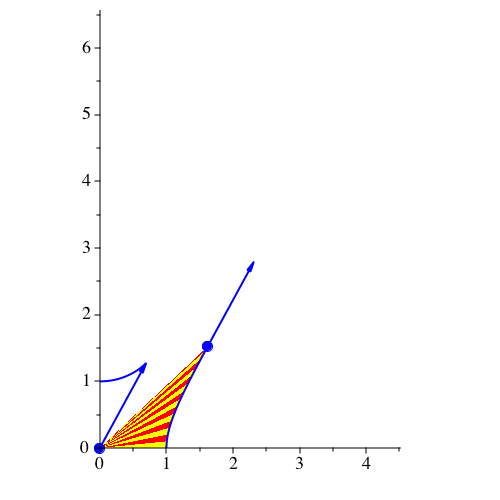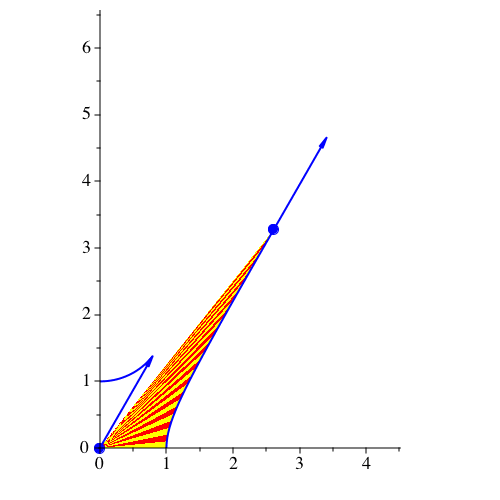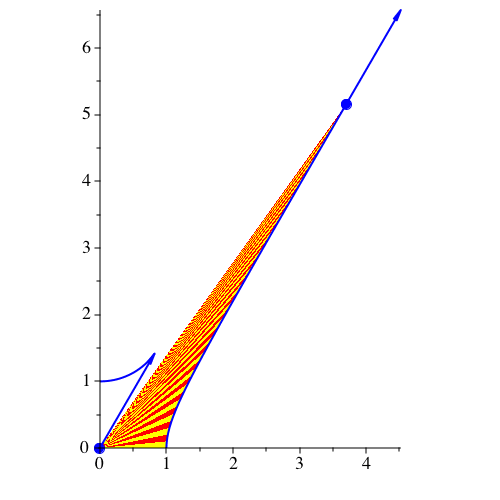
Abb. 21: Abgewandte Hyperbel. vy[0] = 1, G = –1, k = 2, dt = 0.02, dp = 5, N = 200

In der Abbildung 22 sind auch die vom zweiten Brennpunkt ausgehenden Sektoren eingezeichnet. Deren Fläche ist nicht konstant (Tab. 2).

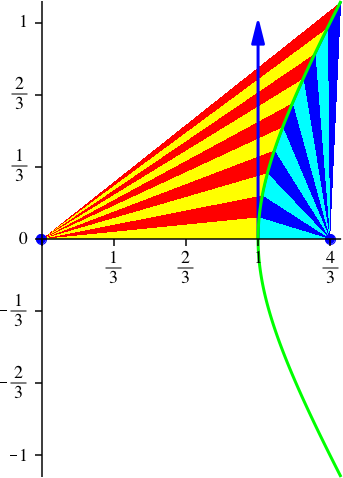
Abb. 22: Gegensektoren

Sektornummer	Sektorfläche rot/gelb	Sektorfläche blau/zyan
1	0.05249999994	0.01762709690
2	0.05249999995	0.01831347169
3	0.0525000000	0.01956367128
4	0.0524999996	0.02121069283
5	0.0525000002	0.02307799815
6	0.0524999992	0.02501721345
7	0.0525000007	0.02692291735
8	0.0524999990	0.02873057374
9	0.0525000000	0.03040706688
10	0.0524999985	0.03194040238

Tab. 2: Sektorflächen und Gegensektorflächen

Sonderfall: für vy[0] := 1/sqrt(1+sqrt(2)) ergibt sich eine gleichseitige Hyperbel (orthogonale Asymptoten) (Abb. 23).

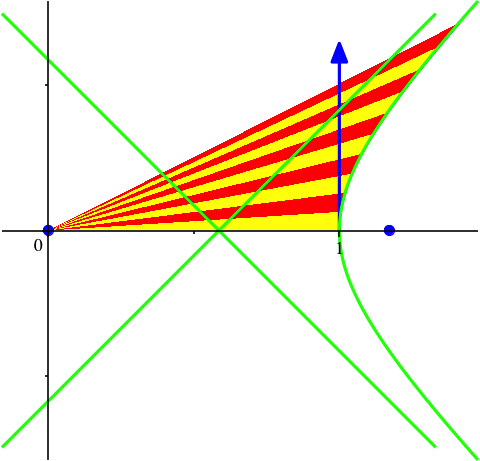
Abb. 23: Sonderfall: gleichseitige Hyperbel

Ich weiß nicht, ob es im abstoßenden Fall auch eine Parabel als Planetenbahn geben kann.

11 Veränderung von k

11.1 Startbedingung für Kreisbahn

Mit den Startwerten

px[0] := 1: py[0] := 0:

vx[0] := 0: vy[0] := 1;

ergibt sich für beliebiges k eine Kreisbahn (vgl. Abb. 12 und 13 für k = 2).

11.2 Andere Bahnen

Wir arbeiten mit den Startwerten:

px[0] := 1: py[0] := 0:

vx[0] := 0: vy[0] := 0.313:

Nun variieren wir k.

Für k = 2 erhalten wir eine Ellipse (Abb. 24).

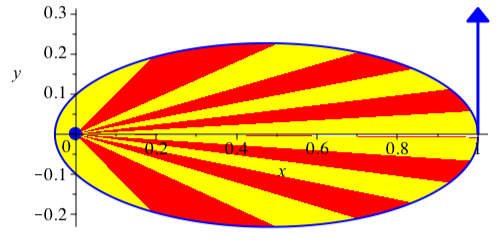
Abb. 24: vy[0] = 0.313, G = 1, k = 2, dt = 0.002, dp = 92, N = 1200. Ellipse mit einem Brennpunkt im Ursprung

Für k = 1 ergibt sich eine Dreierschleife (Abb. 25a).

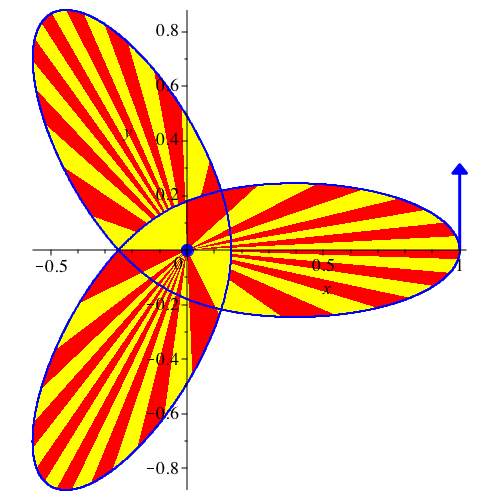
Abb. 25a: vy[0] = 0.313, G = 1, k = 1, dt = 0.002, dp = 82, N = 1400. Kein Kegelschnitt

Die Invarianz der Sektorflächen bleibt erhalten (Tab. 3).

Nr.	Sektorfläche	Nr.	Sektorfläche
1	0.02597900003	26	0.02597899987
2	0.02597900002	27	0.02597899997
3	0.02597899979	28	0.02597899991
4	0.02597899985	29	0.02597899979
5	0.02597899955	30	0.02597900020
6	0.02597899985	31	0.0259790002
7	0.02597900003	32	0.0259790002
8	0.02597900003	33	0.0259789996
9	0.02597900000	34	0.0259790001
10	0.02597899996	35	0.0259789998
11	0.02597900009	36	0.0259790002
12	0.02597900010	37	0.0259790001
13	0.0259790001	38	0.0259790002
14	0.0259789998	39	0.02597900005
15	0.0259790005	40	0.02597900022
16	0.0259789995	41	0.02597900004
17	0.0259789996	42	0.02597900002
18	0.0259789996	43	0.02597899999
19	0.0259789999	44	0.02597899982
20	0.0259789996	45	0.02597899995
21	0.02597900020	46	0.02597900045
22	0.02597899973	47	0.02597900025
23	0.02597899987	48	0.02597899992
24	0.02597899991	49	0.02597900004
25	0.02597899993	50	0.02597900000

Tab. 3: Invariante Sektorflächen

Das Geschwindigkeitsdiagramm ist aber kein Kreis mehr, sondern ebenfalls eine Dreierschleife (Abb. 25b).

Abb. 25b: Geschwindigkeitsdiagramm

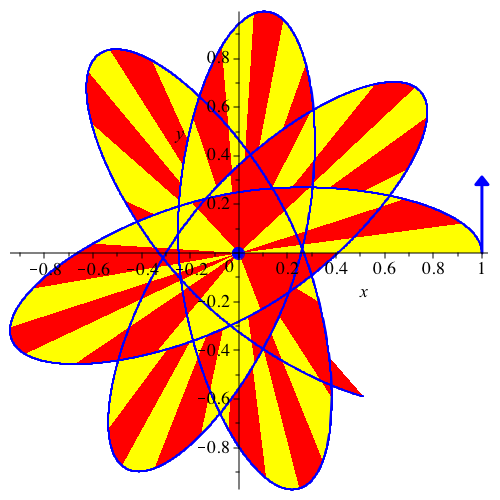
Abb. 26: vy[0] = 0.313, G = 1, k = 0, dt = 0.002, dp = 200, N = 10000. Kein Kegelschnitt

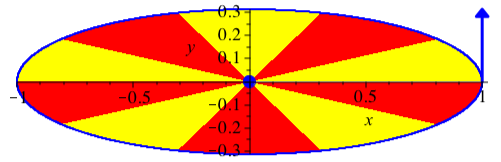
Abb. 27: vy[0] = 0.313, G = 1, k = -1, dt = 0.002, dp = 314, N = 3141. Zentrierte Ellipse

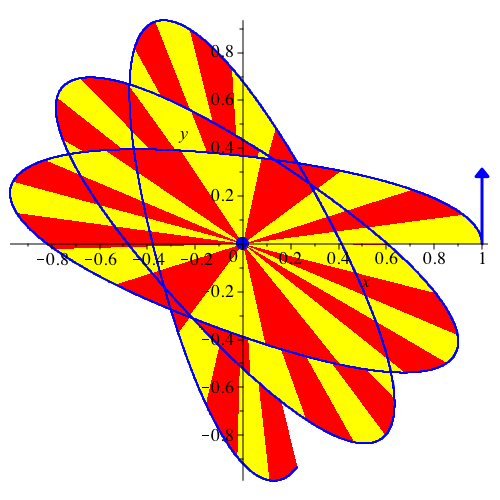
Abb. 28: vy[0] = 0.313, G = 1, k = -2, dt = 0.002, dp = 200, N = 10000. Kein Kegelschnitt

11.3 Federpendel

Mit k = -1 und den Startwerten

px[0] := 0: py[0] := 0:

vx[0] := 0: vy[0] := 1:

ergibt sich das Federpendel (Abb. 29).

Abb. 29: vy[0] = 1, G = 1, k = -1, dt = 2*Pi/500, N = 500. Federpendel