Hans Walser, [20100708a]

Polygonfläche

Anregung: [Bender 2010]

1 Worum es geht

Es werden verschiedene Formeln zur Berechnung des Flächeninhaltes eines einfach geschlossenen Polygons diskutiert. Dabei zeigt sich, dass die Formeln eine gemeinsame Grundlage haben.

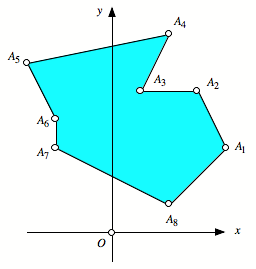
Geschlossenes Polygon mit 8 Eckpunkten

2 Basisformel

Wir verwenden ein kartesischen x-y-Koordinatesystem mit gleich skalierten Achsen und die Bezeichnungen für die Eckpunkte. Damit ist:

Die Summe ist zyklisch, die Indizes sind modulo n zu nehmen.

Diese Formel wurde an den Gymnasien in der Schweiz bis etwa Mitte der achtziger Jahre des 20. Jahrhunderts standardmäßig behandelt. Sie ist heute noch eine beliebte Übungsaufgabe in der linearen Algebra.

Beweis der Basisformel: Für das durch die Ortsvektoren und aufgespannte Parallelogramm oder Dreieck haben wir den orientierten Flächeninhalt:

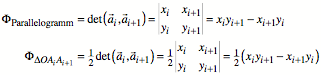
Bei Vertauschung der Ortsvektoren ändert die Orientierung ebenso wie das Vorzeichen der Determinante.

Im Abschnitt 5 sind mehrere schulgemäße Beweise für diese Formeln aufgelistet.

Nun zerlegen wir das Polygon vom Ursprung aus in Dreiecke. Im einfachsten Fall liegt der Ursprung im Innern des Polygons und zwar so, dass wir keine Überlappungen von Dreiecken haben.

Einfachster Fall

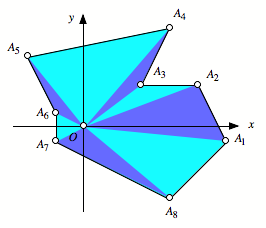
Die Basisformel für den Flächeninhalt ergibt sich sofort und ohne Vorzeichenprobleme. Interessanter ist der Fall, wenn wir vom Ursprung aus gesehen mäandrierende, also rückläufige Randteile haben, oder gar der Ursprung außerhalb des Polygons liegt. In diesen Fällen kommt die Algebra mit den orientierten Flächenteilen zum Tragen. Schülerinnen und Schüler können sich überlegen, wie viele Lagen von positiven und negativen Dreiecken über jedem Punkt liegen. Hier zeigt sich die Eleganz der Algebra.

Rotes Dreieck negativ

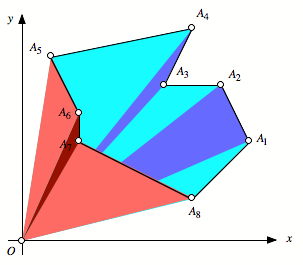
Rote Dreiecke negativ

3 Andere Schreibweisen

Wir gehen aus von der Basisformel:

Der Witz der folgenden Umformungen besteht darin, dass wir eine zyklische Summe haben. Die Indizes sind Modulo n zu nehmen. Wir können daher die Indizes „schieben“, ohne dass sich die Summe ändert. So ist zum Beispiel:

oder

Nun also einige Umformungen. Bei den rot markierten Summen ist der Schiebetrick angewendet worden.

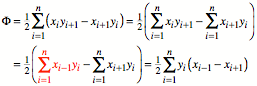
Analog:

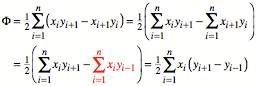
Oder durch Einfügen einer schwarzen Null:

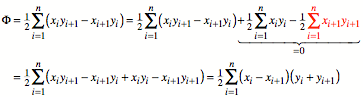
Analog:

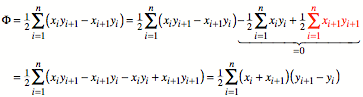
Zusammengefasst haben wir also die vier Formeln (vgl. [Bender 2010], S. 53, 54):

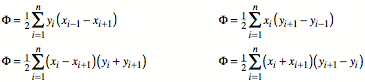
Diese zur Basisformel äquivalenten Formeln haben den rechentechnischen Vorteil, dass sie nur halb so viele Multiplikationen benötigen. Zu Zeiten des Handrechnens war das entscheidend.

4 Aufwärtskompatibilität

Wir berechnen nun den Flächeninhalt eines Gebietes G, dessen Rand eine einfach geschlossene Parameterkurve c ist:

Dazu approximieren wir das Gebiet G durch ein Polygon, indem wir das Parameterintervall in n gleiche Teile unterteilen:

Wir erhalten die Flächenapproximation:

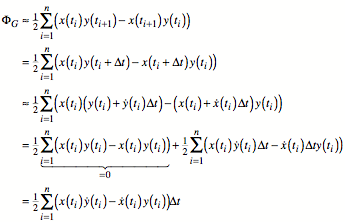
Mit dem Grenzübergang ergibt sich:

Bemerkung: Diese Flächenformel ist ein Spezialfall der Integralformel von Stokes:

Wir setzen dazu das Vektorfeld ein. Es ist linkerseits:

Auf der rechten Seite erhalten wir:

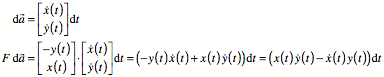
Eingesetzt in die Formel von Stokes ergibt:

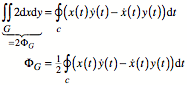
Unsere Basisformel ist also die diskretisierte Form dieser Anwendung der Integralformel von Stokes.

5 Beweise für Parallelogramm- und Dreiecksformel

Wir beweisen jeweils eine der beiden äquivalenten Formeln:

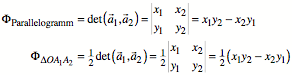
Die Idee dabei ist, einen Sachverhalt unter verschiedenen Aspekten zu sehen und mit verschiedenen Methoden anzugehen.

Die Beweise sind nur skizziert, es muss allenfalls noch die Frage der Orientierung und des Vorzeichens besprochen werden.

5.1 Bildhauermethode

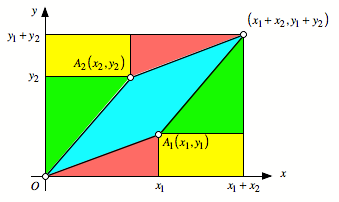
Das Parallelogramm wir aus dem großen Rechteck herausgehauen

Es ist:

5.2 Flächenverwandlungen

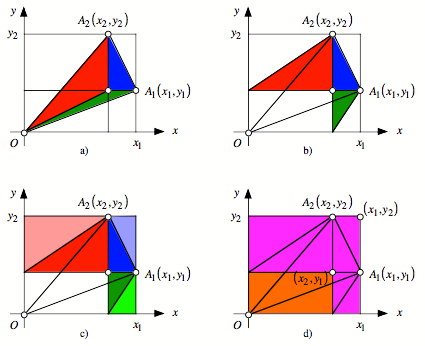
Figurensequenz

Wir berechnen die Dreiecksfläche . Zunächst zerlegen wir das Dreieck in drei Teildreiecke (Figur a) und verscheren zwei davon (Figur b). Nun verdoppeln wir alles (Figur c) und sehen die Flächensumme als Differenzfläche zweier Rechtecke (Figur d). Somit ist:

5.3 Skalarprodukt

Wir arbeiten mit der Flächenformel:

Dabei ist der Zwischenwinkel zwischen den beiden Vektoren, also:

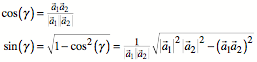
Daraus ergibt sich:

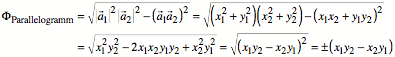
5.4 Additionstheorem

Wir arbeiten wieder mit der Flächenformel:

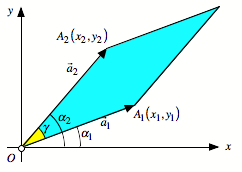
Vektoren und Winkel

Mit bezeichnen wir den Richtungswinkel des Ortsvektors . Es ist:

Wegen ist auf Grund des Additionstheorems für den Sinus:

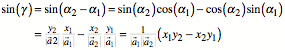
Damit wird:

5.5 Hessesche Normalform

Die Gerade hat die Hessesche Normalform:

Zur Berechnung der Höhe setzen wir die Koordinaten des Punktes ein:

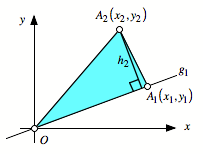
Hessesche Normalform

Nun können wir die Dreiecksfläche berechnen:

5.6 Nochmals Flächenverwandlungen

Wir verwandeln das Parallelogramm in zwei Schritten in ein flächengleiches achsenparalleles Rechteck.

Erster Schritt: Wir scheren rechts nach unten auf die x-Achse.

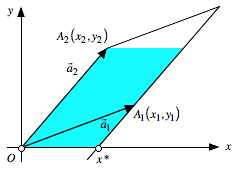
Erster Schritt

Zur Berechnung von muss gelten:

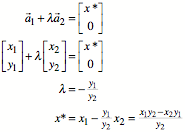
Zweiter Schritt: Wir scheren oben nach links zu y-Achse.

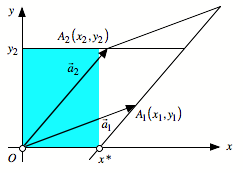
Zweiter Schritt

Nun sehen wir:

Bemerkung: Dieses Verfahren ist eine Visualisierung des Gaußschen Algorithmus zur Berechnung einer Determinante.

5.7 Wer findet weitere Beweise?

Literatur

[Bender 2010] Bender, Peter: Eine einfache Formel für den Flächeninhalt von Polygonen. In: Katja Krüger und Philipp Ullmann (Hg.): Von Geometrie und Geschichte in der Mathematikdidaktik. Festschrift zum 65. Geburtstag von Lutz Führer. Eichstätt: Polygon-Verlag 2010. ISNB: 978-3-928671-60-6. S. 53-70.