Hans Walser, [20231211]
Potenzen
1 Worum geht es
Fortgesetztes Potenzieren mit immer der gleichen Zahl. Assoziativität
2 Erinnerung
2.1 Fortgesetztes Addieren
Es ist:
(a + a) + a = a + (a + a) = 3a
Beim fortgesetzten Addieren spielt die Reihenfolge der Additionen keine Rolle. Die Addition ist assoziativ. Fortgesetztes Addieren des immer gleichen Summanden kann als Multiplikation gedeutet und geschrieben werden.
2.2 Fortgesetztes Multiplizieren
Es ist:
(a • a) • a = a •
(a • a) = a3
Beim fortgesetzten Multiplizieren spielt die Reihenfolge der Multiplikationen keine Rolle. Die Multiplikation ist assoziativ. Fortgesetztes Multiplizieren mit immer dem gleichen Faktor kann als Potenz gedeutet und geschrieben werden.
3 Fortgesetztes Potenzieren
Beim fortgesetzten Potenzieren spielt die Reihenfolge eine Rolle. Das Potenzieren ist nicht assoziativ. Beispiele:
Zwar ist:
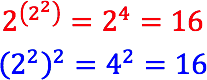
Hingegen ist:
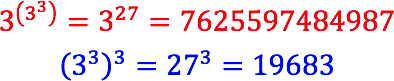
Hier spielt die Assoziativität nicht mehr.
Die Abbildung 1 zeigt in rot beziehungsweise blau die Funktionsgrafen von
![]()
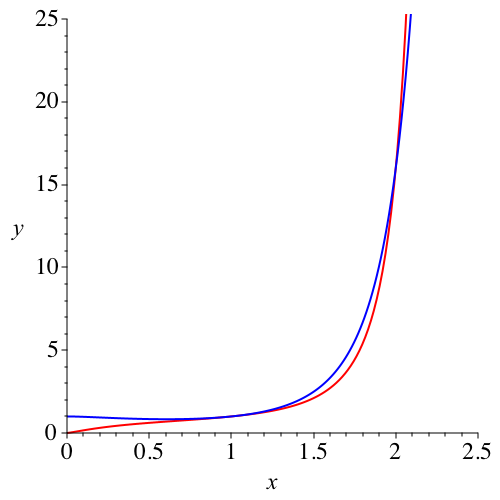
Abb. 1: Funktionsgrafen
Bei x = 1 und x = 2 haben die beiden Funktionen den gleichen Funktionswert, nämlich 1 beziehungsweise 16. Ansonsten sind die beiden Funktionen verschieden.
Es ist nicht sinnvoll, von „fortgesetztem Potenzieren“ zu reden.