Hans Walser, [20160505]
Potenzen der Fibonacci-Zahlen
0 Worum es geht
Es werden die Folgen der Potenzen der Fibonacci-Zahlen bezŸglich Rekursion und expliziter Formel untersucht. Mitteilung von Ergebnissen.
1 Die Fibonacci-Folge
Wir arbeiten mit der verallgemeinerten Fibonacci-Folge an mit den Startwerten
(1)
und der Rekursion:
(2)
FŸr p = 1 und q = 1 ergibt sich die Ÿbliche Fibonacci-Folge.
FŸr unseren allgemeinen Fall erhalten wir:
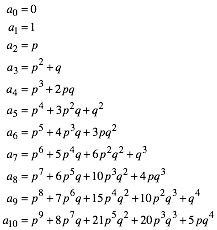(3)
Das Koeffizientendreieck ist ein affin verzerrtes Pascal-Dreieck der Binomialkoeffizienten. Die Spalten sind schrittweise je um eine Zeile nach unten verschoben.
Die Zeilensummen sind die gewšhnlichen Fibonacci-Zahlen.
Die Koeffizienten bei a3 passen entsprechend ins Pascal-Dreieck.
Die Koeffizienten bei a4 sind in umgekehrter Reihenfolge die Anzahlen der Bauteile einer Strecke (2 Punkte, 1 Strecke).
Die Folge hat die explizite Darstellung:
(4)
2 Quadrate der Fibonacci-Zahlen
Es sei:
(5)
Damit gilt:
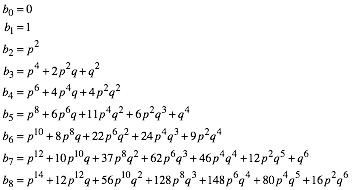(6)
Die Koeffizienten bei b3 passen entsprechend ins Pascal-Dreieck.
Die Koeffizienten bei b4 sind in umgekehrter Reihenfolge die Anzahlen der Bauteile eines Quadrates (4 Ecken, 4 Kanten, 1 Quadrat).
Die Folge bn hat die Rekursion:
(7)
Wir benštigen also drei Startwerte.
FŸr die explizite Formel finden wir:
(8)
3 Dritte Potenzen der Fibonacci-Zahlen
Es sei:
(9)
Damit gilt:
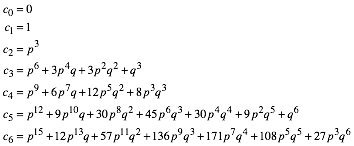(10)
Die Koeffizienten bei c3 passen entsprechend ins Pascal-Dreieck.
Die Koeffizienten bei c4 sind in umgekehrter Reihenfolge die Anzahlen der Bauteile eines WŸrfels (8 Ecken, 12 Kanten, 6 Seitenquadrate, 1 WŸrfel).
Die Folge cn hat die Rekursion:
(11)
Wir benštigen also vier Startwerte.
FŸr die explizite Formel finden wir:
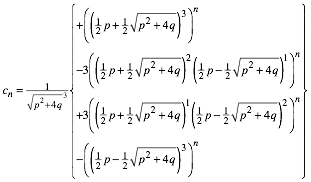(12)
4 Vierte Potenz
Es sei:
(13)
Damit gilt:
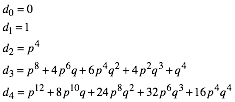(14)
Die Koeffizienten bei d3 passen entsprechend ins Pascal-Dreieck.
Die Koeffizienten bei d4 sind in umgekehrter Reihenfolge die Anzahlen der Bauteile eines 4d-HyperwŸrfels (16 Ecken, 32 Kanten, 24 Seitenquadrate, 8 SeitenwŸrfel, 1 HyperwŸrfel).
5 Sonderfall Fibonacci-Zahlen
Wir setzen p = 1 und q = 1.
Damit erhalten wir folgendes.
5.1 Die Potenzen
Die Tabelle 1 zeigt die ersten Potenzen. Sie gibt auch die Startwerte fŸr die Rekursionen.
|
n |
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
3 |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
|
4 |
1 |
3 |
9 |
27 |
81 |
243 |
729 |
2187 |
|
5 |
1 |
5 |
25 |
125 |
625 |
3125 |
15625 |
78125 |
|
6 |
1 |
8 |
64 |
512 |
4096 |
32768 |
262144 |
2097152 |
|
7 |
1 |
13 |
169 |
2197 |
28561 |
371293 |
4826809 |
62748517 |
Tab. 1: Potenzen der Fibonacci-Zahlen
5.2 Die Rekursionen
Es gelten die Rekursionen.
(15)
Jetz ischÕs so spot wie geschter um die Zyt.
(16)
Klassische Fibonacci-Rekursion.
(17)
Dreigliedrige Rekursion.
(18)
Viergliedrige Rekursion.
(19)
(20)
(21)
(22)
5.3 Zahlendreieck zur Rekursion
Wir schreiben die Rekursionen in der geschlossenen Form wie zum Beispiel (19) neu:
(23)
Damit erhalten wir auf der linken Seite ein Koeffizienten-Dreieck gemŠ§ Abbildung 1.
1
1 –1
1 –1 –1
1 –2 –2 1
1 –3 –6 3 1
1 –5 –15 15 5 –1
1 –8 –40 60 40 –8 –1
1 –13 –104 260 260 –104 –13 1
1 –21 –273 1092 1820 –1092 –273 21 1
Abb. 1: Koeffizienten-Schema
Wir nummerieren wie beim Pascal-Dreieck der Binomialkoeffizienten (also zeilen- und schrŠgspaltenweise je mit null beginnend).
FŸr die Koeffizienten Gn,k gilt:
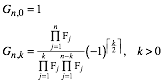(24)
Das Bildungsgesetz erinnert an die Binomialkoeffizienten.
Die Abbildung 2 zeigt dasselbe Zahlen-Dreieck ohne die negativen Vorzeichen.
1
1 1
1 1 1
1 2 2 1
1 3 6 3 1
1 5 15 15 5 1
1 8 40 60 40 8 1
1 13 104 260 260 104 13 1
1 21 273 1092 1820 1092 273 21 1
Abb. 2: Zahlendreieck ohne Vorzeichen
FŸr diese Zahlen Hn,k gilt:
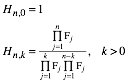(25)
Weiter gilt die Rekursion:
(26)
5.4 Die expliziten Formeln
In den expliziten Formeln erscheint der Goldene Schnitt. Wir verwenden dazu die Schreibweise:
(27)
Es ist:
(28)
(29)
(30)
(31)
5.5 Wurzeln von Gleichungen
Wir bauen aus den rekursiven Formeln Gleichungen in x und berechnen deren Wurzeln.
Aus (15) machen wir:
(32)
Die Lšsung ist nicht weiter interessant:
(33)
Aus (16) machen wir:
(34)
Wir haben die beiden Lšsungen:
(35)
Das sind die beiden Basen in der expliziten Formel (28).
Aus (17) machen wir die kubische Gleichung:
(36)
Diese kubische Gleichung hat die drei Lšsungen:
(37)
Das sind die drei Basen in der expliziten Formel (29).
Aus (18) machen wir die Gleichung vierten Grades:
(38)
Diese hat die vier Lšsungen:
(39)
Das sind die vier Basen in der expliziten Formel (30).
Aus (19) machen wir die Gleichung fŸnften Grades:
(40)
Diese hat die fŸnf Lšsungen:
(41)
Das sind die fŸnf Basen in der expliziten Formel (31).
Wir sehen, wie der Hase lŠuft.
5.6 Funktionsgrafen
Wir definieren die Funktionen:
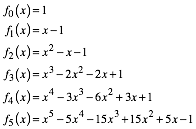(42)
Die Koeffizienten sind dem Schema der Abbildung 1 entnommen. FŸr diese Funktionen erhalten wie die Funktionsgrafen der Abbildung 3.
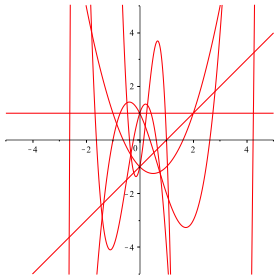
Abb. 3: Funktionsgrafen
Wir erkennen einige Schnittpunkte von jeweils drei Kurven.