Hans Walser, [20210925]
Propeller
1 Worum geht es?
Kinematische Geometrie
2 Propeller
Wird ein Propeller um seinen Mittelpunkt gedreht (Abb. 1), beschreiben die Endpunkte natürlich einen Kreis. Denkt man.
Abb. 1: Propeller
Es kann aber auch anders aussehen (Abb. 2).
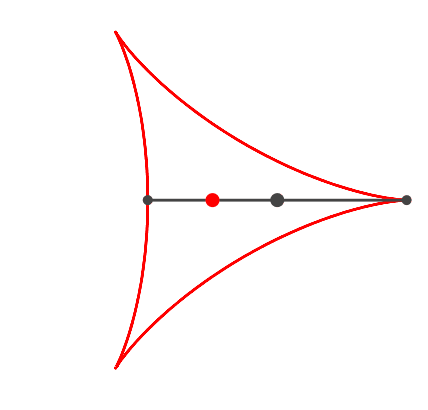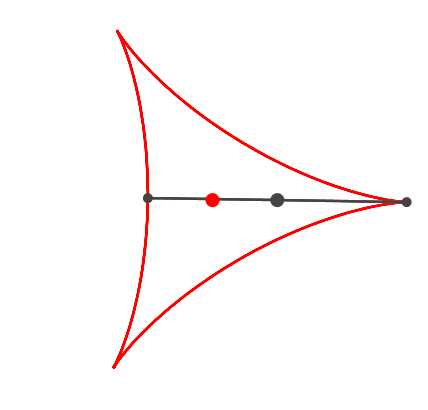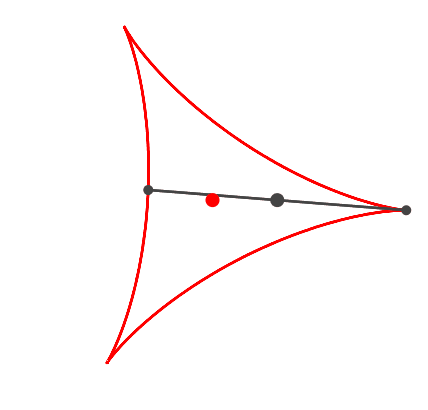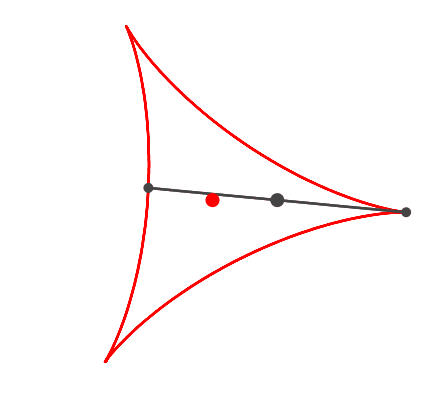
Abb. 2: Dreispitz
Der Witz der Sache ist, dass das Zeichenpapier gleichzeitig mit der
Propellerdrehung um den roten Punkt gedreht wird. Allerdings langsamer als der
Propeller. Wir haben das Drehverhältnis (Frequenzverhältnis) Propeller
: Dreispitz = 3 : 2.
3
Weitere
Beispiele
Es gibt ungezählte weitere Beispiele. Im Folgenden eine kleine Auswahl.
Das einfachste Beispiel ist das orthogonale Kreuz (Abb. 3). Es ergibt
sich unmittelbar aus der Idee des Thaleskreises. Das
Frequenzverhältnis ist 2 : 1.
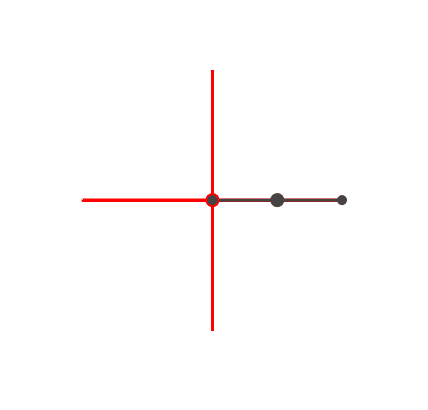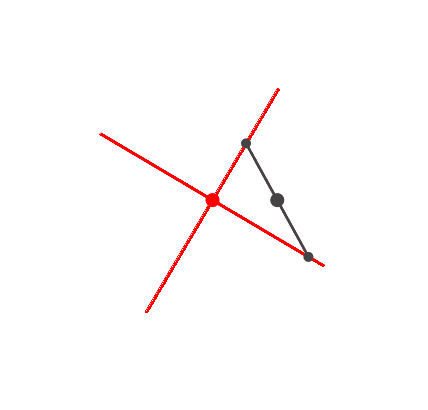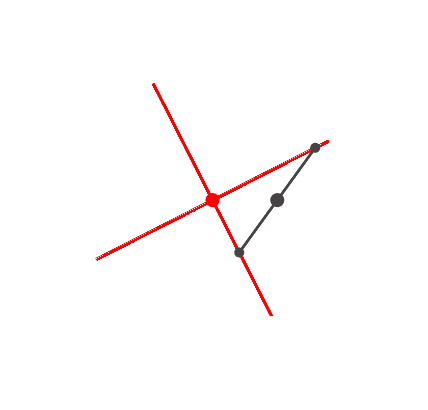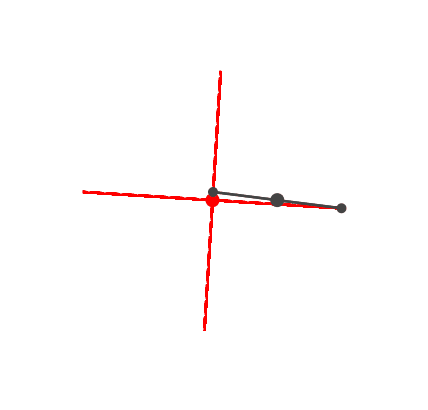
Abb. 3: Kreuz
Die Abbildung 4 zeigt ein orthogonales Ellipsenpaar.
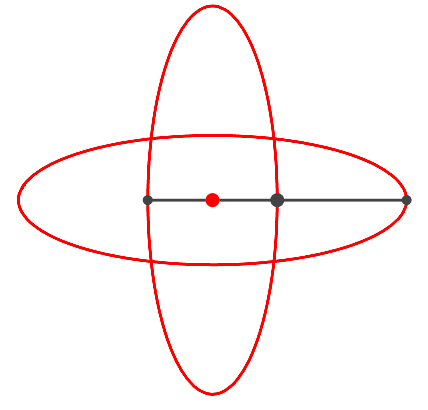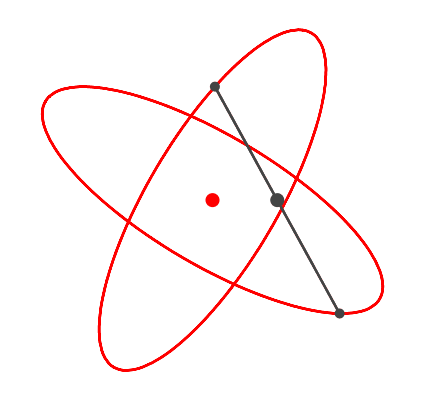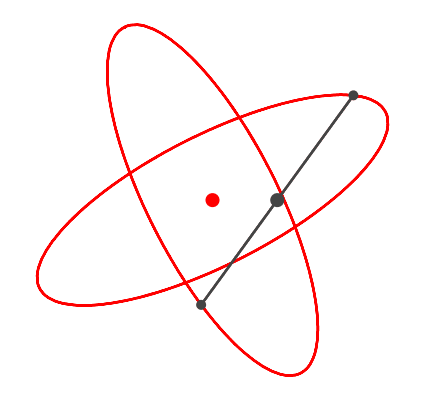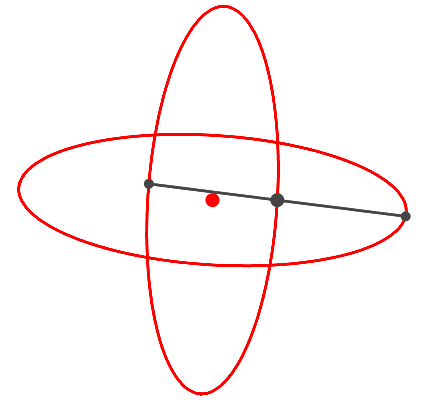
Abb. 4: Ellipsenpaar
Die Abbildung 5 zeigt eine fünfteilige Rosette.
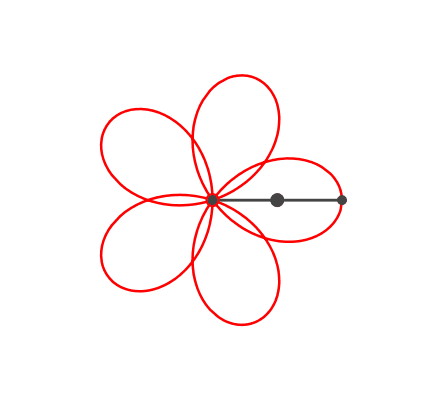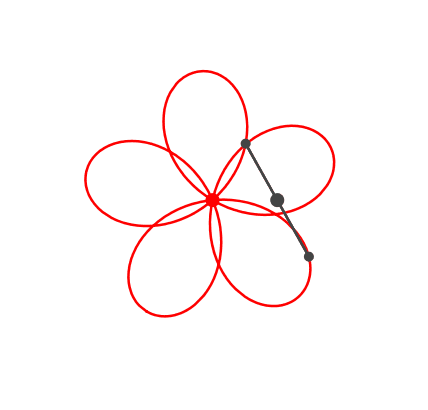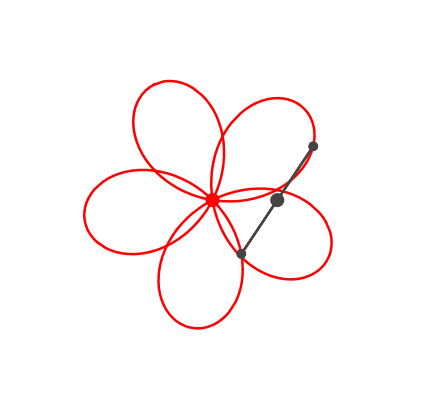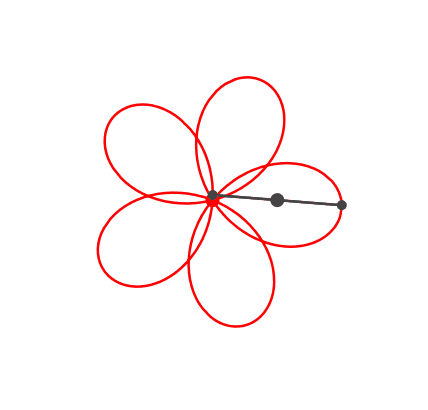
Abb. 5: Rosette
Die Rosette kann auch neunteilig sein (Abb. 6).
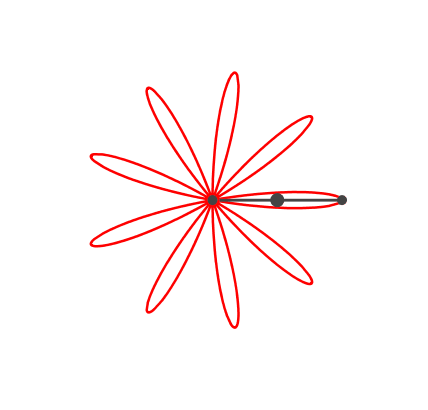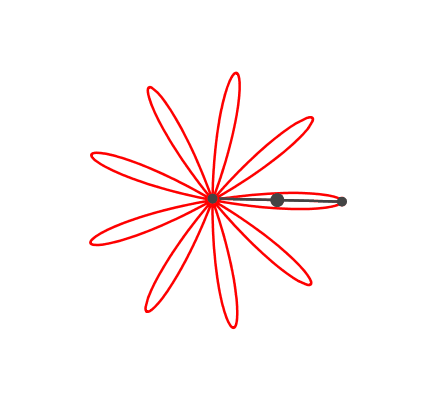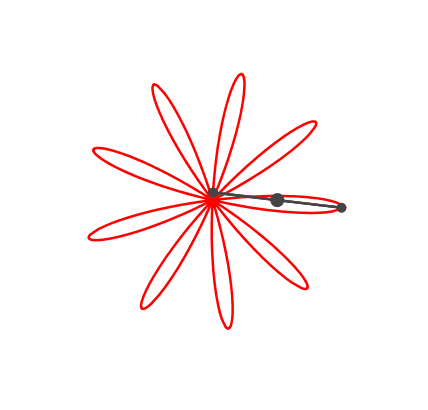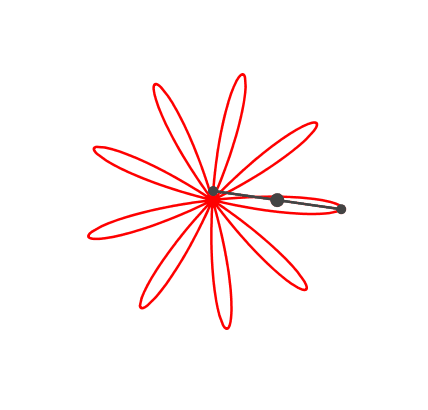
Abb. 6: Neunteilige Rosette
Auch ein gotischer Siebenpass ist möglich (Abb. 7).
Abb. 7: Siebenpass
Und die Kardioide kommt auch vor (Abb. 8).
Abb. 8: Kardioide
4
Formeln
Die Bahnkurven haben als Standbilder folgende Parameterdarstellung:
(1)
Kurve(cos(-n t) + R cos(k
t), sin(-n t) + R sin(k t), t, 0, 2π)
Also:
(2)
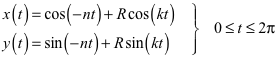
Dabei sind R der Propellerradius und n und k ganze
Zahlen. Das Frequenzverhältnis ist (n + k) :
n.
Die gezeigten Beispiele sind mit den Daten der Tabelle 1 gezeichnet.
|
Abbildung |
R |
k |
n |
|
2 |
2 |
2 |
4 |
|
3 |
1 |
2 |
2 |
|
4 |
2 |
1 |
1 |
|
5 |
1 |
1 |
4 |
|
6 |
1 |
5 |
4 |
|
7 |
8 |
–1 |
8 |
|
8 |
2 |
–2 |
4 |
Tab. 1: Daten für die Beispiele
Die Bahnkurven sind die Überlagerung von zwei Kreisbewegungen.
5
Ausblick
Der Propeller ist nur die Spitze des Eisbergs. Wir können den Propeller
durch ein regelmäßiges Vieleck ersetzen. Die Abbildung 9 zeigt ein regelmäßiges
Fünfeck in einer siebenteiligen Rosette.
Abb. 9: Fünfeck statt Propeller
Websites
Hans
Walser: Al-Sijizi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi/index.html
Hans
Walser: Die Herzkurve und die Möndchen des Hippokrates
www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve_u_Hippokrates/Herzkurve_u_Hippokrates.htm
Hans
Walser: Herzkurve als Enveloppe
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve3/Herzkurve3.htm
Hans Walser: Kardioide
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide5/Kardioide5.htm
Hans Walser: Kardioide
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide6/Kardioide6.htm
Hans Walser: Kardioide
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide8/Kardioide8.htm
Hans Walser: Kardioide als Enveloppe
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide4/Kardioide4.htm
Hans Walser: Kardioide als Spiegelbild der
Parabel bei Kreisspiegelung
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide2/Kardioide2.htm
Hans Walser: Kardioide als Spiegelbild der
Parabel bei Kreisspiegelung
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide2/Kardioide2.htm
Hans Walser: Kardioide und Goldener Schnitt
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide/Kardioide.htm
Hans Walser: Kardioide und regelmäßige
Vielecke
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide3/Kardioide3.htm
Hans Walser: Kardioide und Thaleskreis
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide7/Kardioide7.htm
Hans
Walser: Rosetten
http://www.walser-h-m.ch/hans/Miniaturen/R/Rosetten/Rosetten.html
Hans Walser: Rosetten
http://www.walser-h-m.ch/hans/Miniaturen/R/Rosetten3/Rosetten3.html
Hans Walser: Rosetten
http://www.walser-h-m.ch/hans/Miniaturen/R/Rosetten2/Rosetten2.html
Hans Walser:
Rosettengetriebe
http://www.walser-h-m.ch/hans/Miniaturen/R/Rosettengetriebe/Rosettengetriebe.html
Hans Walser: Umkreis bei regelmäßigen
Vielecken
http://www.walser-h-m.ch/hans/Miniaturen/U/Umkreis/index.html